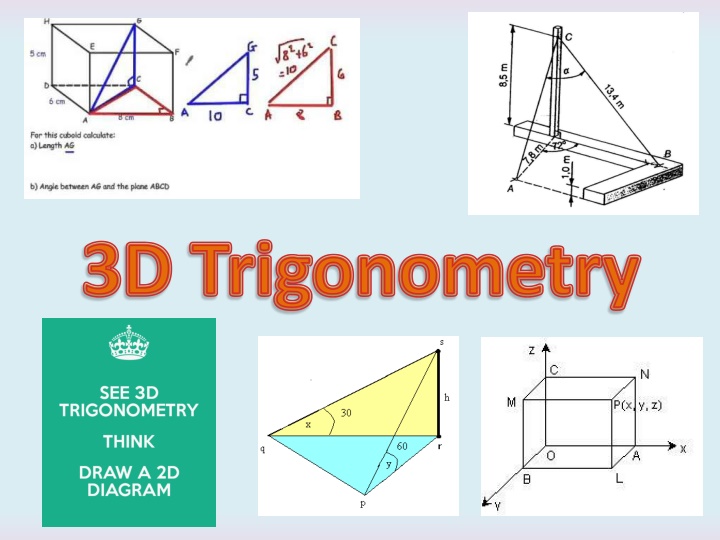
3D Trigonometry
Various 3D trigonometry problems and solutions, ranging from finding missing angles and lengths in triangles to applying trigonometric principles in three-dimensional shapes like cuboids. Understand key concepts by visualizing separate parts of the problems in 2D and making quick sketches. Dive into scenarios such as determining the length of a cuboid's diagonal or calculating angles in pyramid structures like the Great Pyramid of Giza. Enhance your trigonometry skills with practical examples and step-by-step analyses.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
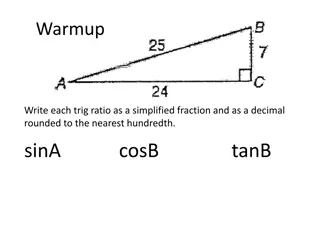
Starter Can you find the value of x in this diagram to 2dp? Be careful with rounding answers! 1) Start by finding the opposite side in the left triangle 3) Then you can find the angle x by using the opposite and hypotenuse in the upper triangle NOT TO SCALE Hyp ??? = ???? ??? ???? =??? 13cm ??? = ???42 8 ??? x 49.82 ??? = 7.20 (2??) ???? =9.93 Opp 5.93 13 2) Then subtract this from the hypotenuse of the lower triangle 4cm ???? = 0.764 42 5.93 ??? ???? ??? = ? = 49.82 8cm Adj 7.20 12 Hyp ??? = Opp ???24 24 ??? = 13.14 (2??) 12cm Adj ?????? ???? = 13.14 7.20 = 5.93
3D Trigonometry We have looked at using trigonometry in lots of situations Today we will be focusing on using it in 3D problems The key to answering questions in 3D is thinking about separate parts of them in 2D You will find that making quick sketches as you work will help you visualise what to do!
3D Trigonometry ABCDEFGH is a cuboid, as shown. a) Calculate the length of BD b) Calculate the angle between BH and the base of the cuboid 8.06cm ( 65) You can find the length of BD by just using the base H G 4cm E F 7cm D C ?2+ ?2= ?2 6cm Sub in values 4cm 72+ 42= ?2 Add up A B 7cm 65 = ?2 Square root 8.06 = ? (Remember that as an exact value, c = 65!)
3D Trigonometry ABCDEFGH is a cuboid, as shown. a) Calculate the length of BD b) Calculate the angle between BH and the base of the cuboid 8.06cm ( 65) To find the angle between BH and the base, draw on BH, and look to make a right angled triangle (inside the shape) H G Opp 6 E F D C 65 6cm Adj 4cm ???? =??? 65 ??? Sub in values A B 6 7cm ???? = 65 Calculate ???? = 0.744 Use inverse Tan ? = 36.7
Plenary The great pyramid of Giza is a square based pyramid of side length 230m, and is 139m high. If you were to stand in one corner and walk up the pyramid to the top, what angle would you be walking up at and how far would you have to walk? We need the length of the diagonal first ?2+ ?2= ?2 Sub in values 2302+ 2302= ?2 230m Add up 105800 = ?2 Square root 230m 325.27 = ? 230m 325.27m 230m
Plenary The great pyramid of Giza is a square based pyramid of side length 230m, and is 139m high. If you were to stand in one corner and walk up the pyramid to the top, what angle would you be walking up at and how far would you have to walk? Now we can draw the height on, and halve the length we just found 139m ???? =??? ??? Opp Sub in values 139 162.63 ???? = 139m Calculate ???? = 0.854 40.5 Use inverse Tan 230m ? = 40.5 325.27m 162.63m 162.63m Adj 230m So you would be walking up at an angle of 40.5
Plenary The great pyramid of Giza is a square based pyramid of side length 230m, and is 139m high. If you were to stand in one corner and walk up the pyramid to the top, what angle would you be walking up at and how far would you have to walk? Now we can draw the height on, and halve the length we just found So you would be walking up at an angle of 40.5 139m ?2+ ?2= ?2 139m Sub in values 162.632+ 1392= ?2 40.5 Add up 230m 45771 = ?2 162.63m 162.63m Square root 213.9 = ? 230m So you would have to walk a distance of 213.9m to the top!
Summary We have looked at using Trigonometry in 3D shapes We have seen how to model this using 2D diagrams We have seen that diagrams help a lot!!
Starter (printout) Can you find the value of x in this diagram to 2dp? Be careful with rounding answers! NOT TO SCALE 13cm x 4cm 42 8cm 24 12cm
Plenary (printout) The great pyramid of Giza is a square based pyramid of side length 230m, and is 139m high. If you were to stand in one corner and walk up the pyramid to the top, what angle would you be walking up at and how far would you have to walk?