7.4 Inverse Trig Functions

Learn about the diverse applications of inverse trigonometric functions in various fields such as actuarial science, aerospace engineering, mechanics, economics, and more. Understand the criteria for a function to have an inverse and explore the inverse sine, cosine, and tangent functions along with their practical uses. Delve into finding exact values without a calculator and evaluating trigonometric functions to three decimal places. Enhance your understanding of how these functions are utilized by professionals in different industries.

• Trigonometry
• Inverse Functions
• Applications
• Engineering
• Mathematics

fitzwater_h Follow

Uploaded on Feb 21, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. 7.4 Inverse Trig Functions Who uses this? Actuaries Aerospace Engineers Mechanical Engineers Nuclear Engineers Economist Boilermakers

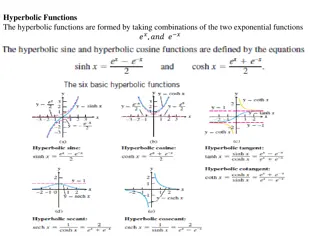
2. For a function to have an inverse it must be one-to-one. One-to-one functions have to pass the horizontal line test. Each y-value can be paired with no more than one x-value. And each x-value can be paired with no more than one y- value. Are the graphs of the trig functions one-to-one? Inverse Sine Function We can make the sine function one-to-one by restricting the domain. For y = sinx the domain is all real numbers and the range is [-1, 1]. To find the inverse we are going to reflect the restricted sine graph over the line y = x.

4. y = sin-1x "the angle between - and with a sine of x." 2 2 Domain: 1,1 Range: , 2 2

5. Ex sin-1 What angle between and has a sine that is ? 2 2 6 Range of the inverse is restricted to right side of unit circle.

6. Find the exact values without a calculator! 1 2 1 1 und sin sin 3 6 2 3 arcsin arcsin 4 3 2 2 1 2 sin ( 1) arcsin 2 1 6

7. Use your calculator to evaluate to 3 decimal places. (You must be in radians!!!) 0.961 sin-1(0.82) 0.309 arcsin(-0.3042) 9.145 cot[sin-1(-0.1087)]

8. Inverse Cosine y = cos-1x or y = arccosx 1,1 Domain: Range: 0,

9. y = cos-1x means the angle in the interval between 0 and pi whose cosine is x. Values of the inverse cosine are located in the upper half of the unit circle.

10. Find the exact values without a calculator! 1 2 und 1 1 cos cos ( 2) 3 3 arccos 5 6 3 2 arccos 4 2 2 ( ) 0.0349 1.001 1 1 cos(cos (0.7)) csc cos 0.7

11. Inverse Tangent y = tan-1x or y = arctanx Domain: or (- , ) Range: , 2 2 The vertical asymptotes become horizontal asymptotes when we reflect the graph over the line y = x. The values are on the right side of the unit circle.

13. Find the exact values without a calculator! tan 1 tan 1 1 3 4 3 3 ( ) arctan arctan 6 20 3 1.521 ( ) 0.1308 1.009 1 arctan(tan ) sec tan und 2

14. Domain of Compositions of Trig Functions [ ( )] x = 1 f f x x = If 1 If 1 1, then sin(sin 1, then cos(cos 1 ) x x = x 1 ) x x = 1 If , then tan(tan ) x x x = 1 [ ( )] f x f x = If -2 If 1 , then sin (sin ) x x x 2 , then cos (cos ) = 0 1 x x x = If -2 1 , then tan (tan ) x x x 2

15. Find the exact value, if it exists. 1 2 1 2 1 sin sin 5 1 sin sin 4 4 und arctan tan2 2 arcsin sin 3 3

16. Find the exact value if it exists. ( ) ( ) 2 sin 2 45 ( sin 90 1 sin 2cos 2 ) 1 ( ) + 1 2 os 90 c cos 120 3 ) 0 + 1 1 cos cos 0 sin ( 1 2

17. Find the exact value without a calculator. 2 3 3 5 1 cos sin 2 = cos 3 5 1 2 1 2 = tan 1 tan sin 5 5 1

18. Write as an algebraic expression in x. ( ) sin(cos-1x) = 1 c ) 2 1 os co s x = 1 cos ( cos 2 sin u u = 1 cos u x ) ( 2 = 1 1 cos x = 1 x 2 OR = = 1 co s Let cos x 1 1 x 2 x x

19. Write as an algebraic expression in x. ( ) tan(cos-1x) 2 1 1 cos cos x 2 sin cos 1 cos cos u u u = = = tan u ( ) u 1 cos cos x = 1 cos u x 2 1 x x = OR = = 1 co s Let cos x 1 1 x 2 x 2 1 x x = tan x

20. Write as an algebraic expression in x. ( ) cos(arcsinx) = 1 s 2 1 in si n x = 1 sin 2 cos u u = 1 sin u x = 1 x 2 OR 1 x = = 1 si n x Let sin x 1 x 2

21. 7.4 b Inverse Trig Functions Sec, csc, cot

22. y = sin-1x y = cos-1x Domain: 1,1 1,1 Domain: Range: 0, Range: , 2 2 y = csc-1x y = sec-1x [1, ) Domain: ( , 1] Domain: ( , 1] [1, ) Range: , , 0 y Range: 0, , y 2 2 2 y = tan-1x Domain: ( y = cot-1x , ) Domain: ( Range: 0, , ) ( ) Range: , 2 2

23. Find the exact values without a calculator! 1 2 csc und ( ) 6 1 1 csc 2 3 ( ) 2 3 3 6 2 arcsec 4 arcsec ( ) 3 1 cot ( 1) arccot 0 4 2

24. Use your calculator to evaluate to 3 decimal places. (You must be in radians!!!) 0.582 csc-1(1.82) arcsec(-5.3042) 1.760 0.322 tan[cot-1(-3.1087)]

25. Find the exact value, if it exists. 3 ( ) ( ) 2 1 sin sec 2 5 und 1 sin csc 4 0 arctan cot2 3 3 arccot sin 2 4

26. Find the exact value without a calculator. 3 ( ) ( ) = tan 2 2 1 tan sec 3 2 2 1 5 3 4 3 1 cot csc 4 = cot 3 5

27. 7.5 Trig Equations An equation that contains trig functions is called a trig equation. To solve a trig equation we find ALL VALUES of the variable that make the equation true.

28. Ex 2sinx 1 = 0 + + 1 1 1 x = 2sin 2 2 sin x = 1 2 11 5 = = sin , x 2 6 6 = + 2 x k 6 k Z 5 = + 2 x k 6

29. Ex tan2x - 3 = 0 + + 3 3 3 x = 2 tan tan x = x = tan = 3 2 = 1 , 3 3 3 + x k 3 2 = + x k 3 k Z

30. Ex 2sin2x 13sinx + 6 = 0 (2sin 1)(sin x 2sin 1 0 x = 1 + + 2sin x = 2 2 1 sin 2 5 , 6 = 6) 0 x 1 1 x = + sin sin 6 6 x = und 0 6 6 + x = = x = + 2 x k 6 6 k Z 5 = + 2 x k 6

31. Ex 2cos2x 7cosx + 3 = 0 (2cos 1)(cos x 2cos 1 0 x = 1 + + 2cos x = 2 2 1 cos 2 x = cos = 3) 0 3 3 + x x = 0 3 3 + 1 1 x = und cos x = 5 = + 2 x k , 3 3 3 k Z 5 = + 2 x k 3

32. Ex sinx = cosx cos x cos x sin cos x x= 1 x = tan 1 5 = = 1 tan 1 x , 4 4 = + k Z x k 4

33. Ex 3cosx = 2sin2x 3cos x = 2 2cos x + (2cos x x+ = cos x = und cos 2 0 2 x = x = 2cos cos 1 0 1 2 , 2(1 cos 3cos 1)(cos 2 ) x 2 2) = + 0 x x = 0 5 = x 3 3 = + 2 x k 3 k Z 5 = + 2 x k 3

34. Ex 1 + sinx = 2cos2x 1 sin x + = 2 2sin sin x + (2sin 1)(sin x 2(1 sin x x 2 ) x 0 = x+ = x = = x = sin sin 1 0 2sin 1 0 1 2 , = 1 + 1 x = sin 1) 0 5 x = x 2 6 6 = + 2 x k = + 2 x k 6 2 5 = + 2 x k k Z 6

35. Ex 1 sin2x cosx = 0 2sin cos x cos (2sin x x = cos 0 x = 2sin 1 0 = cos 1) 0 x x x = 0 1 2 3 x = sin = , x 2 2 5 = , x 6 6 = + = + 2 2 x k x k 6 2 3 k Z 5 = + 2 x k = + 2 x k 2 6

36. Ex 2 3tan3x tanx = 0 tan (3tan x x x = = = 2 1) 0 x = 2 tan 0 3tan 1 0 1 0, x x = tan 3 5 = , x 6 6 = + 0 x k = + x k 6 5 k Z = + x k 6

37. Ex 3 secxtanx = 4sinx 1 sin cos cos x x sin 4sin 1 sin x = x 2 4sin 3 0 x = 0, sin x 0 = 4sin x = 3 4 x = 2 sin x x= x 2 3 x = sin = 3 sin 4sin 4sin x x x 2 4 2 5 = 3 = 4sin 3sin 0 x x , , , x 3 3 3 3 x = 2 sin (4sin x 3) 0 = + = + x k 0 x k 3 2 = + x k = + k Z 0 x k 3 3

38. Ex 4 cosx + 1 = sinx 2 cos 2cos x + cos 2cos x + 2cos 2cos x + (2cos )(cos x x+ = cos x = cos 1 0 1 x = 3 , 1 sin + = 1 1 cos + = 0 x = 1) 0 x+ = 2 2cos 0 x x x 2 2 x = x 2 2 = 2 x = + = + x k 2 x k 2 k Z

39. Ex 5 2sin3x 1 = 0 [0,2 ] 1 2 x = sin3 5 = 3 , x 6 6 5 = + = + 3 2 3 2 x k x k 6 6 2 5 18 2 k k = + = + x x 18 3 3 13 25 18 5 18 17 18 29 18 = = , , , , x x 18 18

40. Ex 5 ?tan? ? 1 = 0 3 x= tan2 x 3 7 = , 2 6 6 x = + k 2 6 = + k Z 2 x k 3