Advanced Algorithms and Data Structures Complexity Analysis

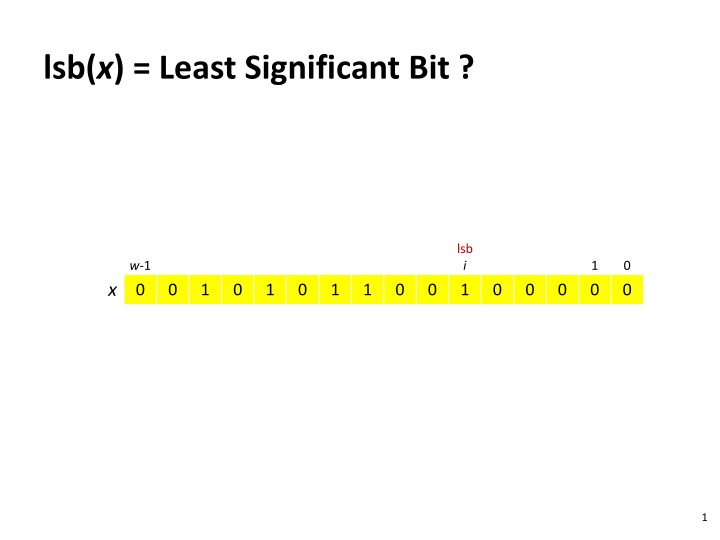
lsb(x) = Least Significant Bit ? lsb i 1 w-1 0 1 0 0 0 x 0 1 0 1 0 1 1 0 0 0 0 0 1

msb(x) in O(1) steps using 5 multiplications [M.L. Fredman, D.E. Willard, Surpassing the information-theoretic bound with fusion trees, Journal of Computer and System Sciences 47 (3): 424 436, 1993] Word size n = g g, g a power of 2

RAM model (Random Access Machine) w bits CPU, O(1) registers 0 010100111010101 1 001010101010111 2 110101010101001 3 111010100101010 4 110110101010101 . 111100011110101 . 111100011111101 111010101010101 111010100101010 110110101010101 111100010000101 111010100101010 110110101010101 100010011110101 000000011111101 100010011110101 000000011111101 000011111111101 111111111111111 - XOR write OR Memory, infinite shift-left + shift-right * read NOT AND not an AC0operation # reads + # writes + # instructions performed Complexity = 3

w/log n x COUNTING-SORT = O(n w/log n) w bits Radix Sort 1 010100111010101 2 001010101010111 3 110101010101001 4 111010100101010 . 110110101010101 . 111100011110101 111100011111101 111010101010101 111010100101010 110110101010101 111100010000101 111010100101010 110110101010101 n 100010011110101 000000000000000 000000000000000 000000000000000 000000000000000 000000000000000 GOAL: Design algorithms with complexity independent of w (trans-dichotomous) [M.L. Fredman, D.E. Willard, Surpassing the information-theoretic bound with fusion trees, Journal of Computer and System Sciences 47 (3): 424 436, 1993] [Cormen et al. 2009] 4

Sorting O(n log n) O(n w/log n) O(n log(w/log n)) O(n loglog n) O(n loglog n) exp. O(n) exp., w log2+ n O(n) exp., w log2n loglog n Comparison Radix-Sort [KR83] [T96] [HT02] [AHNR95] [BBN14] [D. Kirkpatrick, S. Reisch, Upper bounds for sorting integers on random access machines. Theoretical Computer Science 28(3), 1983] [M. Thorup, On RAM Priority Queues. ACM-SIAM Symposium on Discrete Algorithms, 59-67, 1996] [Y. Han, M. Thorup, Integer Sorting in O(n log log n) Expected Time and Linear Space, IEEE Foundations of Computer Science, 135-144, 2002] [A. Andersson, T. Hagerup, S. Nilsson, R. Raman: Sorting in linear time? ACM Symposium on Theory of Computing, 427-436, 1995] [D. Belazzougu, G. S. Brodal, J. A. S. Nielsen, Expected Linear Time Sorting for Word Size (log2n log log n), Scandinavian Workshop on Algorithm Theory, 26-37, 2014] Priority queues (Insert/DeleteMin) O(log n) O(loglog n) O( loglog n) exp. Comparison [T96] [HT02,T07] [M. Thorup, On RAM Priority Queues. ACM-SIAM Symposium on Discrete Algorithms, 59-67, 1996] [Y. Han, M. Thorup, Integer Sorting in O(n log log n) Expected Time and Linear Space, IEEE Foundations of Computer Science, 135- 144, 2002] [Mikkel Thorup, Equivalence between priority queues and sorting, J. ACM 54(6), 2007] 5

Dynamic predecessor searching (w dependent) O(log w) O(log w/loglog w) (static, space nO(1)) O(log w/loglog w loglog n) (dynamic) [vKZ77] [BF02] [P. van Emde Boas, R. Kaas, and E. Zijlstra, Design and Implementation of an Efficient Priority Queue, Mathematical Systems Theory 10, 99-127, 1977] [P. Beame, F.E. Fich, Optimal Bounds for the Predecessor Problem and Related Problems. J. Comput. Syst. Sci. 65(1): 38-72, 2002] [M. Patrascu, M. Thorup, Time-space trade-offs for predecessor search, ACM Symposium on Theory of Computing, 232-240, 2006] Dynamic predecessor searching (w independent) O(log n) O(log n/loglog n) O( log n/loglog n) Comparison [FW93] [AT07] [M.L. Fredman, D.E. Willard, Surpassing the information-theoretic bound with fusion trees, Journal of Computer and System Sciences 47 (3): 424 436, 1993] [A. Andersson, M. Thorup, Dynamic ordered sets with exponential search trees. J. ACM 54(3): 13, 2007] 6

Sorting two elements in one word... ...without comparisons X Y test bit 0 0 1 0 1 0 1 0 0 0 1 1 1 0 0 1 w bits 7

Finding minimum of k elements in one word... ...without comparisons 0 x1 0 x2 0 x3 0 x4 w bits 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 min(x1...x4) Searching a sorted set... 8

Batchers bitonic merger [K.E. Batcher, Sorting Networks and Their Applications, AFIPS Spring Joint Computing Conference 1968: 307-314] [S. Albers, T. Hagerup, Improved Parallel Integer Sorting without Concurrent Writing, ACM-SIAM Symposium on Discrete Algorithms, 463-472, 1992] word implementation, O(log #elements) operations increasing sequence decreasing sequence Round 1 Round 2 Round 3 Round 4 Remark: Sorting networks recently revived interest for GPU sorting 9

van Emde Boas (the idea in the static case) [P. van Emde Boas, R. Kaas, and E. Zijlstra, Design and Implementation of an Efficient Priority Queue, Mathematical Systems Theory 10, 99-127, 1977] min,max 0,13 0,2 13,13 0,2 13,13 0,0 2,2 13,13 2,2 13,13 0,0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Universe U 2w Predecessor search = find nearest yellow ancestor = binary search on path O(loglog U) Space O(U) 10

van Emde Boas (addressing) [P. van Emde Boas, R. Kaas, and E. Zijlstra, Design and Implementation of an Efficient Priority Queue, Mathematical Systems Theory 10, 99-127, 1977] array indexing roots by msb bits min,max 0,13 0,2 13,13 0,2 13,13 002 012 102 112 0,0 2,2 13,13 2,2 13,13 0,0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Universe U 2w 11

van Emde Boas (dynamic) [P. van Emde Boas, R. Kaas, and E. Zijlstra, Design and Implementation of an Efficient Priority Queue, Mathematical Systems Theory 10, 99-127, 1977] 1 recursive top-structure and U bottom structures of the most and least significant log U/2 bits Keep min & max outside structure 1 recursive call min=0, max=13 9 = 2 4 + 1 O(loglog U) search & update 102 012 112 002 12

van Emde Boas (pseudo code) [P. van Emde Boas, R. Kaas, and E. Zijlstra, Design and Implementation of an Efficient Priority Queue, Mathematical Systems Theory 10, 99-127, 1977] succ(i) { i = a n + b } if i > max then return + if i min then return min if size 2 then return max if bottom[a]. size > 0 and bottom[a].max b then return a n + bottom[a].succ(b) else if top.max a then return max c := top.succ(a + 1) return c n + bottom[c].min insert(i) if size = 0 then max := min := i if size = 1 then if i < min then min := i else max := i if size 2 then if i < min then swap(i, min) if i > max then swap(i, max) { i = a n + b } if bottom[a].size = 0 then top.insert(a) bottom[a].insert(b) size := size + 1 delete(i) if size = 2 then if i = max then max := min else min := max if size > 2 then ifi = min then i:= min := top.min n + bottom[top.min].min else ifi = max then i:= max := top.max n + bottom[top.max].max { i = a n + b } bottom[a].delete(b) if bottom[a].size = 0 then top.delete(a) size := size 1 O(loglog U) 13

van Emde Boas (linear space) [P. van Emde Boas, R. Kaas, and E. Zijlstra, Design and Implementation of an Efficient Priority Queue, Mathematical Systems Theory 10, 99-127, 1977] [Dan E. Willard, Log-logarithmic worst-case range queries are possible in space (N), Information Processing Letters 17(2): 81 84, 1983] 9 = 2 4 + 1 min=0, max=13 112 102 012 002 Buckets = lists of size O(loglog U), store only bucket minimum in vEB (Dynamic perfect) Hashing to store all O(n) non-zero nodes of vEB O(n) space, O(loglog U) search 14

O(nloglog n) Sorting [M. Thorup, On RAM Priority Queues. ACM-SIAM Symposium on Discrete Algorithms, 59-67, 1996] loglog n recursive levels of vEB bottom of recursion log U / log n bit elements subproblems of k elements stored in k/log n words mergesort O(k log k loglog n / log n) #elements per word merging 2 words merge-sort O(loglog n) priority queue [M. Thorup, On RAM Priority Queues. ACM-SIAM Symposium on Discrete Algorithms, 59-67, 1996] log n min in single word vEB Sorted lists of size 2i in 2i/w words 15

O( log n) Dynamic predecessor searching [Arne Andersson, Sublogarithmic Searching Without Multiplications. IEEE Foundations of Computer Science, 655-663, 1995] [Arne Andersson, Mikkel Thorup, Dynamic Ordered Sets with Exponential Search Trees, J. ACM 54(3): 13, 2007] vEB - log n recursive levels w / 2 log nbit elements packed B-tree of degree = 2 log n and height log n / log = log n ... ... ... degree search keys sorted in one word O(1) time navigation at node 16 16

Sorting in O(n) time ? 17

Dynamic perfect hashing [Michael L. Fredman, J nos Koml s, Endre Szemer di, Storing a Sparse Table with O(1) Worst Case Access Time, J. ACM 31(3): 538-544, 1984] [Martin Dietzfelbinger, Anna R. Karlin, Kurt Mehlhorn, Friedhelm Meyer auf der Heide, Hans Rohnert, Robert Endre Tarjan, Dynamic Perfect Hashing: Upper and Lower Bounds, SIAM J. Computing 23(4): 738-761, 1994] x h(x) Prime p U (=2w) H = { hk | 0<k<p hk(x) = k x mod p } Pr[ h(x)=h(y) ] = 1/table-size E[ i|Bi|2] = O(n2/table-size) n 1 2 3 i hi(x) pr. (1) no collision in bucket |Bi|2 1 2 3 x pr. (1) total bucket space O(n) no collisions 2-level hashing of set S of size n Random hash functions from H: h, h1, h2, (mod table size) Bucket Bi= { x S | h(x) = i } Rehash: whole table if i|Bi|2 c n new table size n bucket if collision new bucket size |Bi|2 Search O(1) worst-case & updates O(1) expected amortized all hash functions new one new hi 18