Advanced Robotics - Computed Torque Control by Sangsin Park, Ph.D.
Explore the concept of Computed Torque Control in Advanced Robotics through an in-depth explanation by Sangsin Park, Ph.D. This involves feedback linearization, feedforward and feedback loops, derivation of control laws, and PD/PID controllers for outer loop stability.
Uploaded on | 3 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
ME729 Advanced Robotics - Computed-Torque Control 4/16/2018 Sangsin Park, Ph.D.
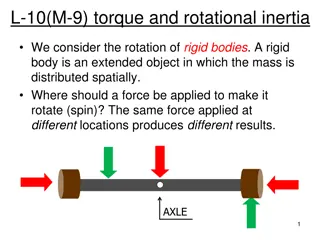
Sangsin Park, Ph. D. Computed-Torque Control Introduction A special application of feedback linearization of the nonlinear system. Feedforward loop : for eliminating nonlinear terms of the system. Feedback loop : for tracking a reference input. Linear system Nonlinear inner loop ?(?, ?) + ?, ? + + ? ?(?) ?? Arm ? Outer loop feedback
Sangsin Park, Ph. D. Computed-Torque Control Derivation of inner feedforward loop The robot dynamics: ? + ? ?, ? + ? ? = ? ? ? For convenience, ? ?, ? + ? ? = ? ?, ? : ? + ? ?, ? = ? ? ? Define tracking error: ? ? = ??? ? ? where, ??? is a desired trajectory. Differentiate the error twice: ? = ?? ?,and ? = ?? ? To eliminate nonlinear term and track a desired trajectory, define the computed-torque control law: ? = ? ?? ? + ? , where ? is the outer loop feedback control input. Substituting into the robot dynamics: ? ? + ? = ? ?? ? + ? ? ?? ? = ?? ? = ? Therefore, if we select a control ? that stabilizes ? = ?, then ? goes to zero.
Sangsin Park, Ph. D. Computed-Torque Control PD controller for the outer loop One way to select the outer loop feedback control input ?is the PD feedback, ? = ?? ? ??? Then the control law becomes ? = ? ??+ ?? ? + ??? + ? The closed-loop error dynamics are ? + ?? ? + ??? = 0 The error system is asymptotically stable as long as the ?? and ?? are all positive.
Sangsin Park, Ph. D. Computed-Torque Control PD controller for the outer loop Block diagram for PD computed-torque controller. ?(?, ?) ?? + + + + ? + ?? ?(?) ?? Arm + ? + ?? ?? ? Feedback loop (or linear controller) Feedforward loop (or linearization)
Sangsin Park, Ph. D. Computed-Torque Control PID controller for the outer loop PD computed-torque control is very effective if all the arm parameters are known and there is no disturbance. it gives a nonzero steady-state error. Consequently, we add an integral controller in the feedback loop. ? = ?? ? ??? ?? ? Then the control law becomes ? = ? ??+ ?? ? + ??? ?? ? + ?
Sangsin Park, Ph. D. Computed-Torque Control PID controller for the outer loop Block diagram for PID computed-torque controller. ?(?, ?) ?? + + + + ? + ?? ?(?) ?? Arm + ? + + ?? ?? + ?? ?? ? Feedback loop (or linear controller) Feedforward loop (or linearization)
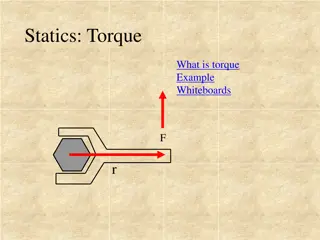
Sangsin Park, Ph. D. Computed-Torque Control For example The two-link planar manipulator. Take the link masses as 1 kg and their lengths as 1 m. ?2 ?2 ?2 ?2 ?1 ?2 ?1 ?1 ?? ?1 ?1 ?? ?? ? The manipulator s equations of motion ? = ? ? ? + ? ?, ? 2 ?1 ?2+ 2?2 ?2 ?1 ?2 3 + 2?2 1 + ?2 1 + ?2 1 ?1 ?2 = + 2?2 ?1
Sangsin Park, Ph. D. Computed-Torque Control For example Rewrite the manipulator s equations of motion ? = ? ? 1{? ? ?, ? } The PD computed-torque control law is given as ??+ ?? ? + ??? + ? ?, ? ? = ? ? ? = ?? ? Let the desired trajectory ?? ?1?= 0.1sin?? ?2?= 0.1cos?? Differentiate the desired trajectory ?1?= 0.1?cos?? ?2?= 0.1?sin?? ?1?= 0.1?2sin?? ?2?= 0.1?2cos?? Set the gains as ??= 100,??= 20
Sangsin Park, Ph. D. Computed-Torque Control For example Simulink blocks System - Manipulator theta1_d_ddot theta_d_ddot y u q theta2_d_ddot M_inv q_dot u y u y y u M V1 V Matrix Multiply 1 s 1 s Matrix Multiply tau theta1_d_dot q_ddot q_dot 20 theta_d_dot Product Integrator Integrator1 Joint Angles (rad) Product1 kd theta2_d_dot Switch into matrix multiplication Switch into matrix multiplication Set initial value as [0; 0] Torque inputs (Nm) Set initial value as [0; 0] theta1_d 100 theta_d kp theta2_d Tracking error (rad)
Sangsin Park, Ph. D. Computed-Torque Control For example Simulation results Yellow line is regarding to ?1. Blue line is regarding to ?2. [Joint angles (rad)] [Tracking error (rad)] [Computed torque input (Nm)]