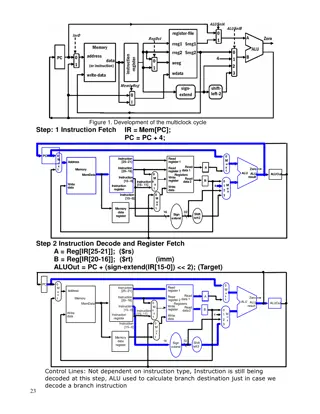
Algorithm Homework Assignment - Strongly Connected Components and Minimum-Cost Spanning Tree
Explore the execution of the strongly connected components algorithm on a directed graph and analyze the impact of adding an edge. Additionally, understand the limitations of a flawed algorithm for computing the minimum-cost spanning tree in a weighted undirected graph. Learn about the importance of edge sorting and the application of Kruskal's Algorithm for optimal results.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Algorithms 2015 Algorithms 2015 Homework Assignment #9 Willy Chang, Wei-Shao Tang 2015.06.16
Problem 3. (a) Run the strongly connected components algorithm on the directed graph shown in Figure 1. (10pt) When traversing the graph, the algorithm should follow the given DFS numbers. Show the High values as computed by the algorithm in each step. 1 (b) Add the edge (4, 2) to the graph and discuss the changes this makes to the execution of the algorithm. (10pt) 4 9 7 2 6 8 5 3
(a) Vertex 1 2 3 4 5 6 7 8 9 DFS_N 9 8 7 6 5 4 3 2 1 1 9 - - - - - - - 1 - 2 9 8 - - - - - - - 4 9 3 9 8 7 - - - - - - 4 9 8 7 6 - - - - - 7 2 6 3 9 8 7 6 - - - - - 5 9 8 7 6 5 - - - - 8 8 5 6 9 8 7 6 5 4 - - 3 - 5 9 8 7 6 5 4 - - - 3 9 8 7 6 5 4 - - - 2 9 8 7 6 5 4 - - - 7 9 8 7 6 5 4 3 - - 8 9 8 7 6 5 4 3 2 - 7 9 8 7 6 5 4 3 2 - 9 9 8 7 6 5 4 3 2 9 7 9 8 7 6 5 4 9 2 9 2 9 9 7 6 5 4 9 2 9 1 9 9 7 6 5 4 9 2 9
(a) Vertex 1 2 3 4 5 6 7 8 9 DFS_N 9 8 8 1 7 7 6 6 5 5 4 4 3 3 2 2 1 9 - - - - - - - 1 - 2 9 8 - - - - - - - 4 9 3 9 8 7 - - - - - - 4 9 8 7 6 - - - - - max 7 2 6 3 9 8 7 6 - - - - - 5 9 8 7 6 5 - - - - 8 5 6 9 8 7 6 5 4 - - 3 - max 5 9 8 7 6 5 4 - - - max 3 9 8 7 6 5 4 - - - max 2 9 8 7 6 5 4 - - - 7 8 9 9 8 8 7 7 6 6 5 5 4 4 3 3 - 2 - - max 7 9 9 9 8 8 7 7 6 6 5 5 4 4 3 3 2 2 - max 1 9 max 3 9 7 9 8 7 6 5 4 2 9 max 8 9 2 9 7 6 5 4 9 2 9 max 1 9 9 7 6 5 4 9 2 9
(b) Vertex 1 2 3 4 5 6 7 8 9 DFS_N 9 8 7 6 5 4 3 2 1 1 9 - - - - - - - 1 - 2 9 8 - - - - - - - 4 9 3 9 8 7 - - - - - - 4 9 8 7 8 - - - - - 7 2 6 3 9 8 8 8 - - - - - 5 9 8 8 8 5 - - - - 8 5 6 9 8 8 8 5 6 - - 3 - 5 9 8 8 8 6 6 - - - 3 9 8 8 8 6 6 - - - 2 9 8 8 8 6 6 - - - 7 9 8 8 8 6 6 3 - - 8 9 8 8 8 6 6 3 7 - 7 9 8 8 8 6 6 7 7 - 9 9 8 8 8 6 6 7 7 9 7 9 8 8 8 6 6 9 7 9 2 9 9 8 8 6 6 9 7 9 1 9 9 8 8 6 6 9 7 9
Problem 4. What is wrong with the following algorithm for computing the minimum-cost spanning tree of a given weighted undirected graph (assumed to be connected)? (20pt.) If the input is just a single-node graph, return the single node. Otherwise, divide the graph into two subgraphs, recursively compute their minimum-cost spanning trees, and then connect the two spanning trees with an edge between the two subgraphs that has the minimum weight.
Problem 4. (Cont.) First, how do you even divide a weighted graph? Won t you discard some important edges? What if there are some edges with same weights when concatenating graph? How do you promise that choosing the minimum weight when concatenating could maintain the minimum cost for each subgraph? At least you should SORT all the edges by its weight in ascending order and concatenate MCST according to that. This is the basic greedy idea called Kruskal's Algorithm.
Problem 5. (20pt.) Let G = (V, E) be a directed graph, and let T be a DFS tree of G. Prove that the intersection of the edges of T the edges of any strongly connected component of G form a subtree of T
Problem 5. (cont.) T1 T2 Proof by contradiction Suppose the intersection are two subtrees (T1, T2). Because T1 and T2 are strongly connected component , there is a cross edge from T1 to T2 However, if DFS starts from T1, it will go through the unmarked vertexes in T2 T1 and T2 will be in the same subtree (Contradiction) The original statement proved true.