Analyzing Basketball Team Data
Process of determining a line of best fit for basketball team data, predicting player performance, identifying outliers, and comparing models for accuracy. Learn about residuals and the importance of choosing the best-fit line for more precise predictions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
In previous problems, each team drew a slightly different line of best fit. Today your class will agree on a single line of best fit for any particular situation.
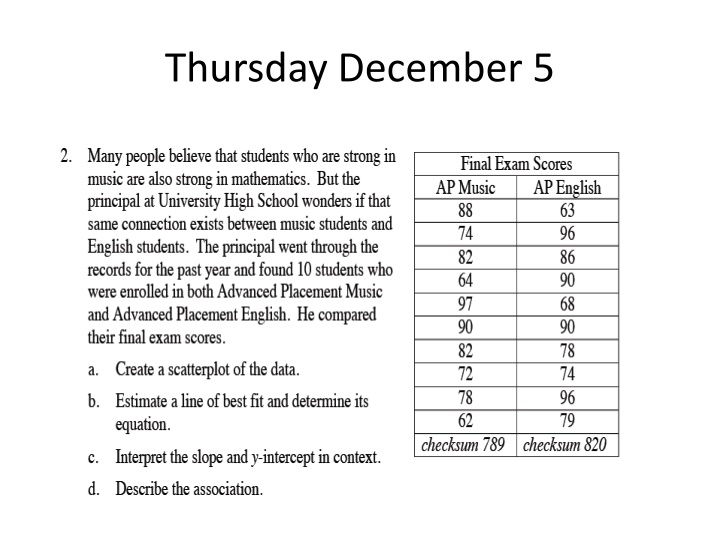
6-30. The following table shows data for one season of the El Toro professional basketball team. El Toro team member Antonio Kusoc was inadvertently left off of the list. Antonio Kusoc played for 2103 minutes. We would like to predict how many points he scored in the season. a) Obtain a Lesson 6.1.4 Resource Page from your teacher or use the Desmos Graph. Draw a line of best fit for the data and then use it to write an equation that models the relationship between total points in the season and minutes played. b) Which data point is an outlier for this data? Whose data does that point represent? What is his residual? c) Would a player be more proud of a negative or positive residual? d) Predict how many points Antonio Kusoc made.
6-31. Different people will come up with different models for the relationship between total points and minutes played in the previous problem. They will also have different estimates for the number of points for Antonio Kusoc. Your Task: Discuss with your team how you can decide which team s equation models the data the best. Compare your team s model to that of another team. Which of the two models is better? Discussion Points: What do you think about when deciding where to place a line of best fit? What makes one line a better model than another line? How can you numerically describe how close the prediction made by the model is to a player s actual total points? Why is thinking about absolute value important in this problem?
6-32. Sometimes there are several different lines of best fit that can be drawn with the same sum of the absolute values of the residuals. To create a single unique line of best fit, statisticians use the sum of the squares of the residuals, instead of the absolute value, to make all the residuals positive. a) What is the sum of the squares of the residuals for your line of best fit b) Compare your result to other teams in your class as directed by your teacher. Did any team have a better model than yours because they had a smaller sum of the squares of the residuals?
Residuals We measure how far a prediction made by our model is from the actual observed value with a residual: residual = actual predicted A residual has the same units as the y-axis. A residual can be graphed with a vertical segment that extends from the point to the line or curve made by the best-fit model. The length of this segment (in the units of the y-axis) is the residual. A positive residual means that the actual value is greater than the predicted value; a negative residual means that the actual value is less than the predicted value.
6-33. A least squares regression line (LSRL) is a unique line that has the smallest possible value for the sum of the squares of the residuals. a) Your teacher will show you how to use your calculator to make a scatterplot. (Graphing calculator instructions can also be downloaded here.) Be sure to use the checksum at the bottom of the table in problem 6-30 to verify that you entered the data into your calculator accurately. b) Your teacher will show you how to find the LSRL and graph it on your calculator. Sketch your scatterplot and LSRL on your paper. c) Your teacher will show you how to find the residuals for the LSRL using your calculator. What is the sum of the squares of the residuals of the LSRL the calculator found? Was it less than your sum of squares? d) How many points does the LSRL predict for Antonio Kusoc? e) Interpret the slope and y-intercept of the model in context. Explain why this LSRL model is not reasonable for players that played less than about 350 minutes.
6-34. Investigate the LSRL and minimizing the squares of the residuals using a computer. a) With your Internet browser, go to http://sambaker.com/courses/J716 /demos/LeastSquares/LeastSquare sDemo.html b) Using the buttons on the right side of the screen, show the residuals and residuals sum, but hide the squares, and the squares sum. Press the mean line button. Your screen should look something like the one at right. Drag the mean line to reduce the sum of residuals. What is the lowest sum of residuals you can get? c)
d) Since there is sometimes more than one line that has the least sum of residuals, mathematicians minimize the sum of the squares of the residuals instead. Using the buttons on the right, show the squares and the squares sum, but hide the residuals, and the residuals sum. Press the mean line button. Your screen should look something like the one at right. e) Drag the mean line to make the squares as small as possible and reduce the sum of squares residuals. What is the lowest sum of squares you can get? f) Press the LS line button to find the LSRL line. There is only one LSRL line that minimizes the sum of the squares. All other lines have a larger sum of squares.