Beta-Cell Modeling Vignette
Glucose modulation, bistability, and feedback mechanisms in beta-cell modeling shed light on the heart of diabetes pathogenesis. Explore the intertwined dynamics of positive and negative feedback, oscillations, and implications for cellular behavior and function. Discover how the Chay-Keizer model, calcium dynamics, and the role of endoplasmic reticulum contribute to understanding beta-cell function. A journey through research milestones and predictions, offering insights into the intricate world of cellular dynamics in health and disease.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Beta-Cell Modeling Vignette Artie Sherman NIH/NIDDK Laboratory of Biological Modeling
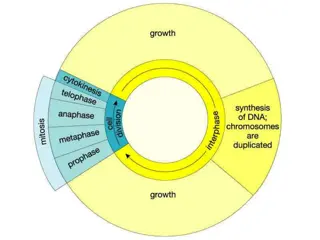
Humble Beginnings A Half Century Ago Glucose modulates plateau fraction of fast bursting Beta-cell failure at the heart of diabetes pathogenesis
Chay-Keizer Model for Bursting Fast positive feedback Slow negative feedback Produces bistability Cell can be spiking or silent at a given value of Ca Biophys. J. 1983 42:181
Chay-Keizer Model Biophys. J. 1983 42:181 dV = C I I I I ( ) ( ) ( ) m Ca K V K Ca K ATP dt ( ) V dn n V n = ( ) dt n dCa = ( ) f I k Ca Ca dt
Bistability Demonstrated by Resetting Cook, Porte, Crill, Am. J. Physiol. 1981, E290
Isolated Rat Somatotroph Looks similar, similar channel mechanism But math says it s different no bistability A missing element in the periodic table of bursting
Effect of Increasing Glucose Increased Ca2+ pump rate Decreased K(ATP) conductance
Calcium Oscillates, but not a Sawtooth Zhang .. Satin, Biophys. J. 84:2852, 2003
Resolve by Adding Endoplasmic Reticulum Jout Cytoplasm Jin Jin,er Jout,er ER Endoplasmic Reticulum
Chay-Keizer with ER Predicted 2004, measured 2011 Ravier et al, Diabetes 60:2533
Summary Positive and negative feedback combine for complex dynamics Threshold Bistability Oscillations Slow variables sweep fast variables through a range of quasi-steady states Bursting Models can be tested by predictions (binary/qualitative) Cycles of prediction and modification Theory goes beyond fitting data to a coherent matrix into which disparate observations can be explained Guides therapy