Binary Tree Node Deletion Strategy
Learn how to efficiently remove nodes from a binary tree. Understand different scenarios such as when a node is a leaf, has one child, or two children. Explore the process of identifying successors and handling parent relationships for effective node removal.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
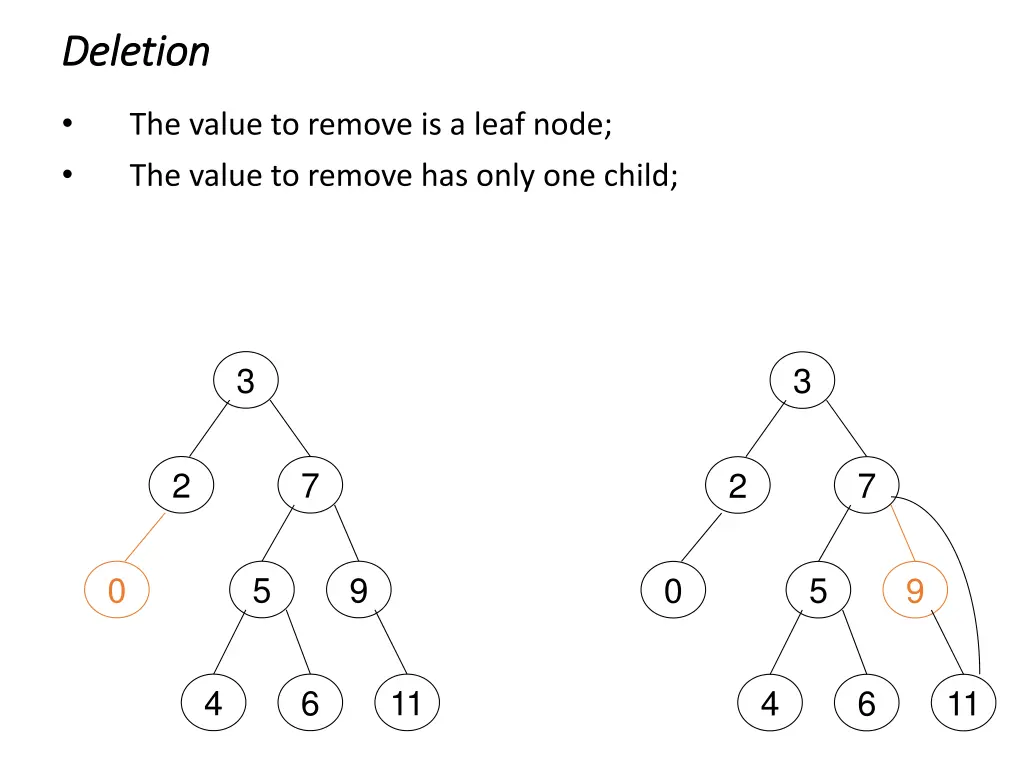
Deletion Deletion The value to remove is a leaf node; The value to remove has only one child; 3 3 2 7 2 7 0 5 9 0 5 9 4 6 11 4 6 11
The value to remove has two children. 3 D is the node that's removed; is the parent of D; R is the successor; PR is the parent of R. 2 7 0 5 9 4 6 11
40 P D is the node that's removed; is the parent of D; R is the successor; PR is the parent of R. D =PR 30 R 20 35 10 R->right=D->right; P->left=R;
P 40 PR->right=R->left; D 30 D is the node that's removed; is the parent of D; R is the successor; PR is the parent of R. 20 33 PR 10 25 35 28 R 3 23 26
Tournament Tree (Winner Tree) Tournament Tree (Winner Tree) https://www.geeksforgeeks.org/wp-content/uploads/Tournament.jpg
Tournament sort Tournament sort A[8]={85, 20, 15, -45, 10, 41, 10, 36} 2k N k=3 85 20 15 -45 10 41 10 36
-45 -45 10 20 -45 10 10 85 20 15 -45 10 41 10 36 -45
10 15 10 20 15 10 10 85 20 15 # 10 41 10 36 -45 10
85 85 85 85 # # # # # # # -45 10 10 15 20 36 41 O(n log2n)
void del(int x) { TREE *dn=NULL; TREE *rn=NULL; //successor if ((dn=find(x,root))==NULL) return; //no right child is easy if (dn->pright==NULL) rn=dn->pleft; //no left is also easy else if (dn->pleft==NULL) rn=dn->pright; //both left and right exist Else { TREE *prn=dn; //parent of successor //find largest element of left subtree rn=dn->pleft; while (rn->pright!=NULL) { prn=rn; rn=rn->pright; } if (prn==dn) {rn->pright=dn->pright; } else {prn->pright=rn->pleft; rn->pleft=dn->pleft; rn->pright=dn->pright; } } if (parent==NULL) root=rn; else if (dn->dann<parent->dann) parent->pleft=rn; else parent->pright=rn; delete(dn); }
TREE *parent=NULL; TREE *find(int x, TREE* ptr) { while (ptr!=NULL) { if (x==ptr->dann) break; else { parent=ptr; if (x<ptr->dann) ptr=ptr->pleft; else ptr=ptr->pright; } } return ptr; }
