Box Plot and Interquartile Range Explanation
A box plot is a graphical representation of data divided into quartiles, showing the spread of the data. Learn about the statistical summaries, including the interquartile range, with examples and visuals. Understand how to interpret and construct box plots for data analysis.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
BOX PLOT Lesson 11-4
WHAT IS BOX PLOT? A graphical representation of a data set as a box in which the data ordered and divided into four intervals or quartiles. Each quartile contains approximately 25% of the data. Q1 ,1st Quartile, 25thpercentile, Lower Quartile: 25% of the data lies below the first quartile Q2, median, 2ndQuartile, 50thPercentile: 50% of the data lies below the second quartile Q3, 3rdQuartile, 75thPercentile, Upper Quartile: 75% of the data lies below the third quartile
EXAMPLE 1: FIND THE 5 STATISTICAL DATA SUMMARY OF THE BOX PLOT Maximum value is 100 Minimum value is 65 Q1=70 Q2 or median =80 Q3=90
INTERQUARTILE RANGE IQR Or Interquartile Range: is a measure of statistical dispersion or spread. It is equal to the difference between the 3rd (upper)quartile and1st (lower) quartile ; Its also called the midspread or middle fifty. IQR = Q3 Q1.
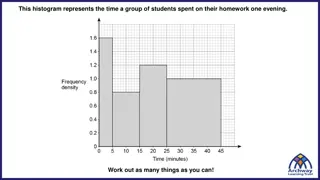
EXAMPLE 2: Shown below are the scores 16 students received on a math quiz. 52, 60, 66, 66, 68, 72, 72, 73, 74, 75, 80, 82, 84, 91, 92, 98 Find the five statistical data summary for this data set Construct a box plot on the number line given below.