Capacitance and Energy Storage in Dielectrics
Exploring the concept of capacitance, potential energy storage in capacitors, and the role of dielectrics. Learn about the calculations, applications, and examples of capacitors in electrical systems.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
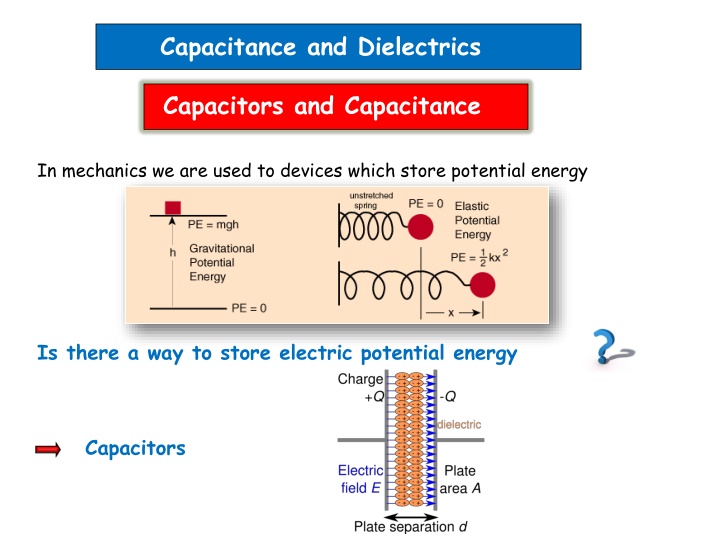
Capacitance and Dielectrics Capacitors and Capacitance In mechanics we are used to devices which store potential energy Is there a way to store electric potential energy File:Capacitor schematic with dielectric.svg Capacitors
Any 2 conductors insulated from each other form a capacitor can be realized by an insulating material (dielectric) or vacuum In circuit diagrams a capacitor is represented by the symbol: Let s charge a capacitor -Q +Q Vab=Va-Vb Vb Va
Remember our electric field calculations for various charged objects 1 Q = x Q 1 E e = = ( , 0) E x y e x 2 2 R ( ) 2 + x / 1 R x 3 4 r 0 0 We always find E Q b = = voltage V V V Q Since V V E dr ab a b a b a Q V Capacitance = C depends only on geometry and dielectric properties, not on charge SI unit 1F=1C/V read F=Farad in honor of Michael Faraday ab Capacitance is an intuitive characterization of a capacitor. It tells you: how much charge a capacitor can hold for a given voltage (potential difference). The more the higher the capacitance
Calculating capacitance Q V According to the major task in calculating C is calculating Vab = C ab ------------------------------------------- Homogeneous field, E= / 0 for the limit d<< plate dimensions +++++++++++++++++++++++++ Parallel-plate capacitor Using b = V V E dr a b Charge density Q A = a / d Qd A = = = V Ed ab 0 0 d We obtain the capacitance C of a parallel-plate capacitor in vacuum as A = 0 C d Note: 1F is a huge capacitance. More typical values are 1 F=10-6F to 1pF=10-12F
A few slightly more involved examples Capacitance of a spherical capacitor Step 1: calculate the electric field using Gauss s law between the 2 spheres Q E d A Q E Q = a r b for = 2 4 E r 0 0 = 2 4 r Image from http://hyperphysics.phy-astr.gsu.edu/hbase/electric/capsph.html Step 2: calculate the voltage Vab for a given amount of charge Q on the spheres b Qdr Q Q V r r a Q C V 1 a 0 b 1 1 a 1 b = = = ab 2 4 4 4 0 0 0 a 4 4 ab a = = = Step 3: applying 0 1 b 0 C b ab
Clicker question Does an isolated (individual) charged sphere have capacitance? 1) No, where would the electric field lines end? 2) Yes, I just don t know the value 4 1 a = 3) Yes, it is a special case of 0 1 b C in the limit b-> Image from http://hyperphysics.phy-astr.gsu.edu/hbase/electric/capsph.html
Capacitance per length of a cylindrical capacitor (coaxial cable) Step 1: calculate the electric field using Gauss s law Q L / Q = E d A 0 Cylinder with a<r<b L L = = E 2 E rL 2 r = / Q L 0 0 Step 2: calculate the voltage Vab b a b dr = = ln V ab 2 r 2 0 a 0 1 C L C L Q 2 C L = 55.6 / pF m = = = Step 3: applying 0 b a b a LV V ln ln ab ab Typical value for antennas, VCRs 69pF/m
Clicker question How did I like the first midterm exam? A) I have a thing for midterms, this one rocked as usually* B) The midterm was hard and unfair. C) The midterm was as expected D) I hate exams and this one was particularly bad. Hate it, hate it, hate it. *