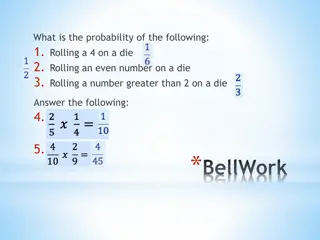Chance and Probability: Exploring Random Events and Statistical Uncertainty
In this lecture series, delve into the realm of chance and probability, understanding random events and the uncertainty they bring. Discover the significance of sample space, events, and Venn diagrams in analyzing outcomes. Gain insights into fields like genetics, medicine, and statistics where chance plays a pivotal role. Explore the interconnectedness between individual differences, diseases, and treatment responses, shedding light on the complexities of probability and its practical applications.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Chance and Probability Part 1 Nina Gunnes September 23, 2021 09/23/2021 Fall 2021 - Lecture 3 1
Chance Something random and unpredictable (i.e., not deterministic) Sex of a child Development of lung or breast cancer Several possible sources Lack of complete knowledge Genetics Uncertainty (e.g., uncertain diagnoses) Measurement error 09/23/2021 Fall 2021 - Lecture 3 2
Chance, cont. Individual differences Proneness to disease Response to treatment Elements of chance reduced by more detailed knowledge about the disease process and personal characteristics Crucial in preventive medicine Subject to certain laws and principles (e.g., the law or large numbers) Creates order in the apparent chaos that constitutes chance Makes it possible to perform mathematical calculations 09/23/2021 Fall 2021 - Lecture 3 3
Chance, cont. Field of statistics Does not remove the random element Valuable insight about the meaning and impact of statistical uncertainty Evaluation of medical treatments and interventions through, e.g., controlled clinical trials http://www.picpedia.org/highway-signs/s/statistics.html 09/23/2021 Fall 2021 - Lecture 3 4
Random experiment Outcome not clearly determined in advance Number of dots when rolling a die Sex of a child at birth Side facing up when flipping a coin Only possible outcomes known beforehand! 09/23/2021 Fall 2021 - Lecture 3 5
Sample space Comprises all possible (mutually exclusive) elementary outcomes of a random experiment Rolling a die ? = 1,2,3,4,5,6 Birth ? = boy,girl Flipping a coin ? = head,tail https://pixabay.com/illustrations/sketch-cartoon-space-set-3045125/ 09/23/2021 Fall 2021 - Lecture 3 6
Event Often denoted by capital letters such as ?, ?, ?, etc. Constitutes a subset of the sample space One or more elementary outcomes E.g., more than three dots when rolling a die: ? = 4,5,6 Occurs if one of the elementary outcomes in the subset occurs Several events may occur simultaneously 09/23/2021 Fall 2021 - Lecture 3 7
Venn diagram Shows relations between different subsets of the sample space Symbolizes the sample space and events ? ? ? ? 09/23/2021 Fall 2021 - Lecture 3 8
Operations on events Example of rolling a die ? = 1,2,3,4,5,6 ? = 1,2,3 ? = 4,5,6 Complement of ?: ?, ? , or ?? All possible elementary outcomes not in ? ? ? ? 09/23/2021 Fall 2021 - Lecture 3 9
Operations on events, cont. Example of rolling a die ? = 1,2,3,4,5,6 ? = 1,2,3 ? = 1,3,5 ? ? = 1,2,3,5 Union of ? and ?: ? ? All possible elementary outcomes in either ? or ? (or both) ? ? ? 09/23/2021 Fall 2021 - Lecture 3 10
Operations on events, cont. Example of rolling a die ? = 1,2,3,4,5,6 ? = 1,2,3 ? = 1,3,5 ? ? = 1,3 Intersection of ? and ?: ? ? All possible elementary outcomes in both ? and ? ? ? ? 09/23/2021 Fall 2021 - Lecture 3 11
Disjoint events Example of rolling a die ? = 1,2,3,4,5,6 ? = 1,2,3 ? = 4,5,6 ? ? = Empty intersection: ? ? = No common possible elementary outcomes in ? and ? ? ? ? 09/23/2021 Fall 2021 - Lecture 3 12
Combining events ? ? ? ? ? ? ? ? ? ? 09/23/2021 Fall 2021 - Lecture 3 13
Probability Linked to an infinite number of repetitions of a random experiment Relative frequency of a specific outcome in the long run Proportion of experiments in which the outcome occurs Probability of event ?, ? ? : ?? ?as ? Total number of experiments: ? Number of experiments in which event ? occurs: ?? Relies on the law of large numbers 09/23/2021 Fall 2021 - Lecture 3 14
Probability model Mathematical description of a random experiment All possible elementary outcomes with associated probabilities Based on reasoning or real observations Probability of the sample space: ? ? = 1 (or 100%) Uniform probability model Each possible elementary outcome in the sample space associated with the same probability E.g., probability of a specific number of dots when rolling a die 09/23/2021 Fall 2021 - Lecture 3 15
Probability calculation Based on a few simple calculation rules Makes it possible to calculate the probability of quite complex events Expressed by using some notation for the number of experiments in which different events occur In total: ? Events ?, ? (i.e., not ?), and ?: ??, ??, and ??, respectively Either event ? or event ? (or both): ?? ? Both event ? and event ?, simultaneously: ?? ? 09/23/2021 Fall 2021 - Lecture 3 16
Probability calculation, cont. Complement rule: ? ? + ? ? = 1 Either ? or ? must occur every time: ??+ ??= ? Relative frequency: ?? ?+ Addition rule for disjoint events: ? ? ? = ? ? + ? ? ? and ? cannot occur at the same time (disjoint events): ?? ?= ??+ ?? Relative frequency: ?? ? ? ? Calculating the probability of an event by adding up the probabilities of the possible elementary outcomes composing it ?? ?= ??+?? ? =? ?= 1 =??+?? =?? ?+?? ? 09/23/2021 Fall 2021 - Lecture 3 17
Probability calculation, cont. General addition rule: ? ? ? = ? ? + ? ? ? ? ? ? and ? sometimes occur at the same time: ?? ?= ??+ ?? ?? ? Relative frequency: ?? ? ? =??+?? ?? ? =?? ?+?? ? ?? ? ? ? ? ? ? 09/23/2021 Fall 2021 - Lecture 3 18
Rolling a die twice (or two dice once) 36 possible elementary outcomes A one on the first roll A two on the first roll A three on the first roll A four on the first roll A five on the first roll A six on the first roll A one on the second roll A two on the second roll A one on the second roll A two on the second roll A one on the second roll A two on the second roll A one on the second roll A two on the second roll A one on the second roll A two on the second roll A one on the second roll A two on the second roll A three on the second roll A four on the second roll A three on the second roll A four on the second roll A three on the second roll A four on the second roll A three on the second roll A four on the second roll A three on the second roll A four on the second roll A three on the second roll A four on the second roll A five on the second roll A six on the second roll A five on the second roll A six on the second roll A five on the second roll A six on the second roll A five on the second roll A six on the second roll A five on the second roll A six on the second roll A five on the second roll A six on the second roll Sample space: ? = 11,12, ,16,21,22, ,26, ,61,62, ,66 09/23/2021 Fall 2021 - Lecture 3 19
Example of rolling a die twice, cont. A six on the first roll: ? = 61,62,63,64,65,66 , where ? ? =1 A six on the second roll: ? = 16,26,36,46,56,66 , where ? ? =1 At least one six on the two rolls: ? = ? ?, where ? ? = ? ? and ? disjoint events? No! A six on both the first and second roll: ? ?, where ? ? ? = General addition rule ? ? = ? ? ? = ? ? + ? ? ? ? ? =1 6 6 1 36 6+1 1 36=11 6 36 09/23/2021 Fall 2021 - Lecture 3 20
Method of counting outcomes Simple and useful method for calculating probabilities Assumes a uniform probability model All possible elementary outcomes in the sample space equally likely Number of possible elementary outcomes corresponding to the event of interest divided by the number of possible elementary outcomes in total # favorable outcomes # possible outcomes 09/23/2021 Fall 2021 - Lecture 3 21
Method of counting outcomes, cont. Example of flipping two coins Two sides on each coin H: head; T: tail Sample size ? = HH,HT,TH,TT Four possible outcomes in total Getting one of each side (i.e., one head and one tail) ? = HT,TH Two favorable outcomes ? ? =2 4= 0.5 https://commons.wikimedia.org/wiki/File:Coin_Toss_(3635981474).jpg 09/23/2021 Fall 2021 - Lecture 3 22
References Aalen OO, Frigessi A, Moger TA, Scheel I, Skovlund E, Veier d MB. 2006. Statistiske metoder i medisin og helsefag. Oslo: Gyldendal akademisk. Wikipedia contributors. Probability theory. Wikipedia, The Free Encyclopedia. September 17, 2019, 07:41 UTC. Available at: https://en.wikipedia.org/w/index.php?title=Probability_theory&oldid=916 140932. Accessed September 18, 2019. Wikipedia contributors. Probability. Wikipedia, The Free Encyclopedia. September 17, 2019, 07:39 UTC. Available at: https://en.wikipedia.org/w/index.php?title=Probability&oldid=916140748. Accessed September 18, 2019. 09/23/2021 Fall 2021 - Lecture 3 23