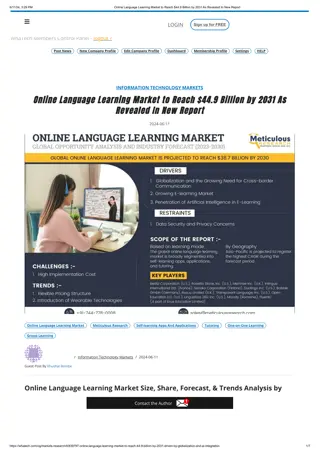
Chemical Reaction Engineering (CRE) Fundamentals

Lecture 3 Chemical Reaction Engineering (CRE) is the field that studies the rates and mechanisms of chemical reactions and the design of the reactors in which they take place.

Lecture 3 Lecture 3 Thursday Thursday Review of Lectures 1 and 2 Building Block 1 Mole Balances (Review) Size CSTRs and PFRs given rA= f(X) Conversion for Reactors in Series Building Block 2 Rate Laws Reaction Orders Arrhenius Equation Activation Energy Effect of Temperature 2 2

Reactor Reactor Mole Balances Mole Balances Summary Summary The GMBE applied to the four major reactor types (and the general reaction A B) Reactor Differential Algebraic Integral NA N dN A 0 A N dN = A t Batch A= r V A r V dt A t V =FA0 FA CSTR rA FA F dF A dFA dV A PFR = A V = rA dr A F 0 V FA F dF A PBR dFA dW A = A W = r A A r F 3 3 0 W

b + d + a A B C c D Choose limiting reactant basis as A of calculatio n b c d + + A B C a D a a moles reacted A = X moles A fed 4

Reactor Reactor Mole Balances Mole Balances Summary In term In terms of Conversion s of Conversion Summary Reactor Differential Algebraic Integral X X dX dX 0 = t N Batch = N r V A A r V 0 A dt A 0 t F X = 0 A V CSTR r A X dX dX 0 = V F = PFR F r 0 A 0 A A r dV A X X dX dX 0 = W F A = PBR F r 0 A A r 0 A dW 5 5 W

Levenspiel Levenspiel Plots Plots 6 6

Reactors in Series Reactors in Series moles of reacted A point to up i Xi= moles of A fed first to reactor Only valid if there are no side streams 7 7

Reactors in Series Reactors in Series 8 8

Building Block 2: Building Block 2: Rate Laws Power Law Model: Rate Laws order in A A B r = kC C A order in B Overall = + Rection Order 9 9

Building Block 2: Building Block 2: Rate Laws Rate Laws + 2 A B 3 C A reactor follows an elementary rate law if the reaction orders just happens to agree with the stoichiometric coefficients for the reaction as written. e.g. If the above reaction follows an elementary rate law A A A C k r = 2 C B 2nd order in A, 1st order in B, overall third order 10 10

Building Block 2: Building Block 2: Rate Laws Rate Laws Rate Laws are found from Experiments 2A+B 3C Rate Laws could be non-elementary. For example, reaction could be: Second Order in A Zero Order in B Overall Second Order 2 A A A r k C = 2 B B A r k C = r k C = 2 A C C 11 11

Relative Rates of Reaction Relative Rates of Reaction + + aA bB cC dD b c d + + A B C D a a a r r r r = = = C A B D a b c d 12 12

Relative Rates of Reaction Relative Rates of Reaction C 3 B A 2 + mol rA = 3 10 Given dm s r r r = = Then C A B 2 1 3 r mol = = 5 A r B 3 2 dm s 3 mol = = 15 r r C A 3 2 dm s 13 13

Reversible Elementary Reaction Reversible Elementary Reaction kA k-A A+2B 3C 3 C = = 2 3 2 C k r k C C k C k C C A A A B A C A A B k A A 3 C 2 = C k C C A A B K e 14 14

Reversible Elementary Reaction Reversible Elementary Reaction kA k-A Reaction is: First Order in A Second Order in B Overall third Order A+2B 3C moles moles CA= = rA 3 dm 3 dm s 3 6 r mole dm s dm k = = = A ( )( ) 2 2 2 C C mole s 3 3 mole dm mole dm A B 15 15

16 16

Algorithm Algorithm How to find ( ) X rA= f ( ) C r = g Step 1: Rate Law A i ( ) Ci= ( ) X h Step 2: Stoichiometry ( ) X rA= f Step 3: Combine to get 17 17

Arrhenius Equation Arrhenius Equation k is the specific reaction rate (constant) and is given by the Arrhenius Equation. where: = E RT k Ae T k A T 0 k 0 A 1013 k T 18 18

Arrhenius Equation Arrhenius Equation where: E = Activation energy (cal/mol) R = Gas constant (cal/mol*K) T = Temperature (K) A = Frequency factor (same units as rate constant k) (units of A, and k, depend on overall reaction order) 19 19

Reaction Coordinate Reaction Coordinate The activation energy can be thought of as a barrier to the reaction. One way to view the barrier to a reaction is through the reaction coordinates. These coordinates denote the energy of the system as a function of progress along the reaction path. For the reaction: A BC A + ::: + ::: B C AB C The reaction coordinate is: 20 20

21 21

Collision Theory Collision Theory 22 22

Why is there an Activation Energy? Why is there an Activation Energy? We see that for the reaction to occur, the reactants must overcome an energy barrier or activation energy EA. The energy to overcome their barrier comes from the transfer of the kinetic energy from molecular collisions to internal energy (e.g. Vibrational Energy). 1. The molecules need energy to disort or stretch their bonds in order to break them and thus form new bonds 2. As the reacting molecules come close together they must overcome both stearic and electron repulsion forces in order to react. 23 23

Distribution of Velocities Distribution of Velocities We will use the Maxwell-Boltzmann Distribution of Molecular Velocities. For a species af mass m, the Maxwell distribution of velocities (relative velocities) is: 3 2 m k T ( ) 2 = 2 mU k T 2 , 4 f U T dU e U dU B 2 B f(U,T)dU represents the fraction of velocities between U and (U+dU). 24 24

Distribution of Velocities Distribution of Velocities A plot of the distribution function, f(U,T), is shown as a function of U: T1 T2 T2>T1 ? ?,? U Maxwell-Boltzmann Distribution of velocities. 25 25

Distribution of Velocities Distribution of Velocities ( ) , f U T dU 3 2 m k T 2 = 2 mU k T 2 4 e U dU Given B 2 B 1mU E = 2 Let 2 E 2 k T ( ) = k T 1 2 , f E T dE E e dE B ( ) 3 2 2 B f(E,T)dE represents the fraction of collisions that have energy between E and (E+dE) 26 26

f(E,T)dE=fraction of molecules with energies between E+dE One such distribution of energies is in the following figure: 27

End of End of Lecture Lecture 3 3 28 28

Supplementary Material Supplementary Material AB BC VBC VAB kJ/ kJ/ Molecule Molecule r0 rBC rAB r0 Potentials (Morse or Lennard-Jones) 29 29

Supplementary Material Supplementary Material One can also view the reaction coordinate as variation of the BC distance for a fixed AC distance: l B l A BC l AB C A C AB r BC r For a fixed AC distance as B moves away from C the distance of separation of B from C, rBC increases as N moves closer to A. As rBC increases rAB decreases and the AB energy first decreases then increases as the AB molecules become close. Likewise as B moves away from A and towards C similar energy relationships are found. E.g., as B moves towards C from A, the energy first decreases due to attraction then increases due to repulsion of the AB molecules as they come closer together. We now superimpose the potentials for AB and BC to form the following figure: 30 30

Supplementary Material Supplementary Material Reference AB S2 S1 BC Energy E* Ea E1P E2P HRx=E2P-E1P r 31 31