Chemical Reaction Engineering: Rates, Mechanisms & Reactor Design
Chemical Reaction Engineering (CRE) delves into the rates, mechanisms, and reactor design of chemical reactions. Explore topics such as Enzymatic Reactions, Michaelis-Menten Kinetics, Enzyme Inhibition, Active Intermediates, and more.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
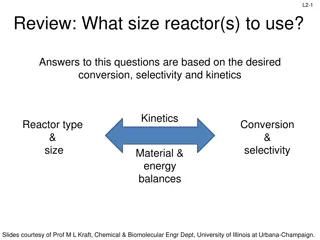
Lecture 15 Chemical Reaction Engineering (CRE) is the field that studies the rates and mechanisms of chemical reactions and the design of the reactors in which they take place.
Lecture Lecture 15 15 Tuesday 3/12/2013 Tuesday 3/12/2013 Enzymatic Reactions Michealis-Menten Kinetics Lineweaver-Burk Plot Enzyme Inhibition Competitive Uncompetitive Non-Competitive 2 2
Review Last Lecture Active Intermediates and PSSH 3 3
Review Last Lecture Active Intermediates and PSSH 1.In the PSSH, we set the rate of formation of the active intermediates equal to zero. If the active intermediate A* is involved in m different reactions, we set it to: = = i m = 0 . * A r r * net A i 1 2. The azomethane (AZO) decomposition mechanism is 2 ( ) k + AZO = rN 1 ( ' k ) AZO 2 By applying the PSSH to AZO*, we show the rate law, which exhibits first-order dependence with respect to AZO at high AZO concentrations and second-order dependence with respect to AZO at low AZO concentrations. 4 4
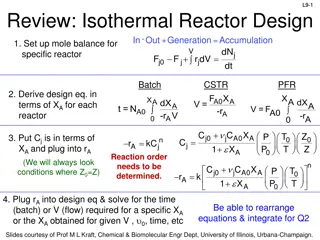
Enzymes Michaelis-Menten Kinetics Enzymes are protein-like substances with catalytic properties. Enzyme Unease [From Biochemistry, 3/E by Stryer, copywrited 1988 by Lubert Stryer. Used with permission of W.H. Freeman and Company.] 5 5
Enzymes Enzymes provide a pathway for the substrate to proceed at a faster rate. The substrate, S, reacts to form a product P. Slow S P E S Fast A given enzyme can only catalyze only one reaction. Example, Urea is decomposed by the enzyme urease. 6 6
Enzymes - Urease A given enzyme can only catalyze only one reaction. Urea is decomposed by the enzyme urease, as shown below. + H + + O NH CONH UREASE 2 NH CO UREASE 2 2 2 3 2 + H2 + O S E P E The corresponding mechanism is: + 1 k k W + + E E E S S S E E S S 2 + k P E 3 7 7
Enzymes - - Michaelis ( )( ) S E k rP = 3 ( )( ) E k r S E = = 1 0 ( )( ) k 2 + ( ) ( E E Et + = Michaelis- -Menten Menten Kinetics Kinetics W ( ) ( ) S k E S k W 3 E S 2 k E S ( ) = 1 E S k W 3 ) S E ( ) E = t k S + 1 1 + k k W 3 2 8 8
Enzymes - - Michaelis Michaelis- -Menten Menten Kinetics Kinetics V k W k + max cat E S k E + S ( )( ) W = = = 3 t cat t r k E S 3 P k k W 3 K S + S 2 M k 1 K M V S ( )( ) W = = max r k E S 3 P + K S m 9 9
Enzymes - - Michaelis Michaelis- -Menten Menten Kinetics Kinetics Vmax=kcatEt Turnover Number: kcat Number of substrate molecules (moles) converted to product in a given time (s) on a single enzyme molecule (molecules/molecule/time) kcat H2O2+ E H2O + O + E For the reaction: 40,000,000 molecules of H2O2converted to product per second on a single enzyme molecule. 10 10
Enzymes - - Michaelis Michaelis- -Menten Menten Kinetics Kinetics Michaelis-Menten Equation V S = = r r max P S + K S M (Michaelis-Menten plot) Vmax V V S = max 2 max / 1 S 2 Solving: + K M / 1 2 -rs KM=S1/2 therefore KMis the concentration at which the rate is half the maximum rate. CS S1/2 11 11
Enzymes - - Michaelis Michaelis- -Menten Menten Kinetics Kinetics 1 1 K 1 = + M Inverting yields: r V V S S max max Lineweaver-Burk Plot 1/-rS slope = KM/Vmax 1/Vmax 1/S 12 12
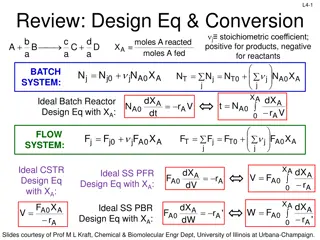
Types of Enzyme Inhibition Competitive + E I I inactive ( E ) Uncompetitive + E S I I E inactive ( S ) Non-competitive + + E S I I E inactive ( S ) I E S I E inactive ( S ) 13 13
Competitive Inhibition 14 14
Competitive Inhibition + + k k E S E S E P 3 1 k 2 + k E I E inactive ( I ) 4 k 5 1) Mechanisms: + + E S E S E S E S + + E S P E E I E I + E I = E I r k C S P 3 E 15 15
Competitive Inhibition 2) Rate Laws: r = = 0 k C C k C k C S S E S 1 S E 2 E 3 E k C C C C = = C 1 S E S E S E + k C k K 2 3 m k C r = 3 S E P K = m k = r 0 C C k C I E 4 I E 5 I E k C C = = C K 5 I E I E I K k 16 16 I 4
Competitive Inhibition C = + + = Etot C C C C C S Etot E E I E E C C + + 1 S I K K k C C m I = 3 Etot S r P C K + + K C I K m m S I V C = r max S S + 1 C + C K I S m K I + 1 1 k C 1 = + 1 m I r V V K C 17 17 S max max I S
Competitive Inhibition From before (no competition): 1 1 1 K = + M r V V C Increasing CI max max S S Competitive Competitive No Inhibition 1 Sr KM + 1 1 1 K C = slope = + 1 M I V r V V K C max max max S I S 1 = Intercept 1 V max C S Intercept does not change, slope increases as inhibitor concentration increases 18 18
Uncompetitive Inhibition 19 19
Uncompetitive Inhibition Inhibition only has affinity for enzyme-substrate complex k 1 + k E S E S P 3 k 2 k 4 + I E S I E S inactive ( ) k 5 Developing the rate law: ( ) = = r r k E S P S cat ( )( ) E ( ) ( ) ( )( I ) ( ) (1) = = ) ) + 0 r k S ( )( I 4 k E S k ( E S k E S k I E S 1 2 4 5 E S cat = = (2) k E S k I E S r 0 5 I E S 20 20
Uncompetitive Inhibition Adding (1) and (2) ( )( ) ( E ( ) ( ( )( ) K ) = 0 k E S k E S k E S 1 2 cat ( )( ) k + 2 k E S E S ) = = 1 S k cat M From (2) ( )( I ) ( )( )( ) K K k E S I E S ( ) ( )( I ) = = = 4 I E S E S k K 5 I I M k = 5 K I k 4 ( )( ) K k E S ( ) = = cat r k E S p cat 21 M
Uncompetitive Inhibition Total enzyme ( ) ( E ) ( + ) = + E E S I E S t ( ) K ( )( ) K K S I S ( ) E = + + 1 M I M ( ) S k E = cat t r ( ) K ( )( ) K K ( ) + 1 p S I S + + 1 K M M I M V S = = max r r ( ) K S P I ( ) S + K M I 22
Uncompetitive Inhibition ( ) K 1 1 I ( ) S = + + 1 K ( ) S M r V max S I ( ) K 1 1 1 K I = + + 1 M ( ) S r V V max max S I Slope remains the same but intercept changes as inhibitor concentration is increased 23 Lineweaver-Burk Plot for uncompetitive inhibition
Non-competitive Inhibition E + S E S P + E +I -I -I +I (inactive)I.E + S I.E.S (inactive) Increasing I 1 V C Sr = No Inhibition max S r S + 1 C ( ) + k C I M S k Both slope and intercept changes I 1 1 1 C k C = + + + 1 1 I M I r V k V C k 1 max max S I S I C S 25 25
Summary: Types of Enzyme Inhibition Lineweaver Burk plots for three types of enzyme inhibition. 26 26
End of Lecture 15 End of Lecture 15 27 27