Community Care Partners Overview
In the realm of behavioral health community care partnerships, Community Care Partners play a vital role in enhancing care coordination for MassHealth members with complex needs. These partners, including Behavioral Health Community Partners (BH CPs) and Long Term Services and Supports Community Partners (LTSS CPs), provide specialized care management and navigation for populations with significant behavioral health and LTSS needs. Community Care Partners is a collaboration of three community-based providers – Vinfen, Baycove, and Bridgewell – offering care coordination services to MassHealth enrollees with complex behavioral, medical, and substance-related needs. Care coordination, facilitated by teams of healthcare professionals, aims to improve overall health and quality of life, empower clients, enhance care experiences, reduce duplicative services, and lower costs. BH CP South Care Team, led by Director of Care Coordination Lisa Goldsmith, exemplifies the dedication and specialization required to fulfill the objectives of care coordination effectively.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
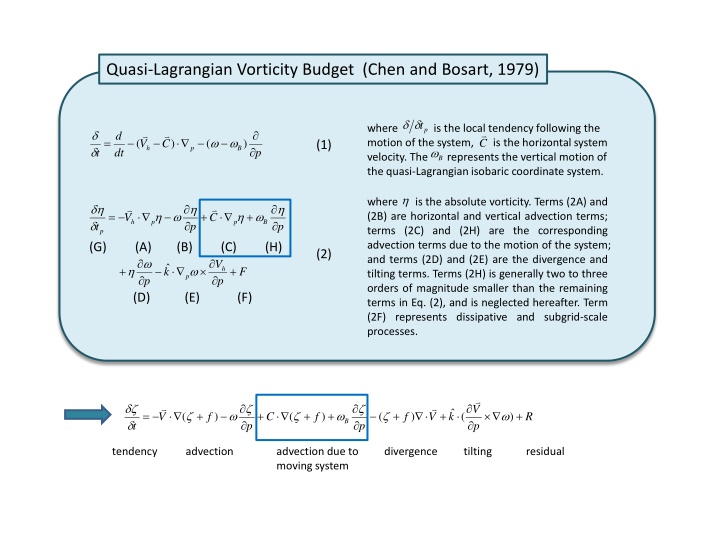
Quasi-Lagrangian Vorticity Budget (Chen and Bosart, 1979) pt where is the local tendency following the motion of the system, is the horizontal system velocity. The represents the vertical motion of the quasi-Lagrangianisobaric coordinate system. d = C V ( ) ( ) C (1) h p B t dt p B where (2B) are horizontal and vertical advection terms; terms (2C) and (2H) are the corresponding advection terms due to the motion of the system; and terms (2D) and (2E) are the divergence and tilting terms. Terms (2H) is generally two to three orders of magnitude smaller than the remaining terms in Eq. (2), and is neglected hereafter. Term (2F) represents dissipative and subgrid-scale processes. is the absolute vorticity. Terms (2A) and = + + V C h p p B t p p p (G) (A) (B) (C) (H) (2) V k + + F h p p p (D) (E) (F) V k = + + + + + + + ( ) ( ) ( ) ( ) V f C f f V R B t p p p tendency advection advection due to moving system divergence tilting residual
for tendency term: = T = 0 = = = = = 1 0 1 2 1 2 t t t t 1 2 t dt t dt + + = = = = 1 2 0 1 1 2 t t t t T = -1 1 2 t t dt dt = 2 2 T = -2 = = = 0 2 t t 2 dt dt1 = = = 0 2 t t 2 t dt dt2 for other terms: + ( ) ( ) V V 1 1 = ( ) 1 2 V = + ( ) ( ) ( ) V V V = = 2 1 0 1 t t 2 1 2 1 1 1 + + ( ) ( ) ( ) V V V = + ( ) ( ) ( ) V V V = = = 0 1 2 t t t 2 2 = = = 2 1 2 t t 2 2 2
TC A TC B TC C TC D TC E TC A total vorticity 1.E-04 8.50E-05 8.00E-05 9.E-05 7.50E-05 8.E-05 7.00E-05 7.E-05 6.50E-05 6.E-05 6.00E-05 5.E-05 5.50E-05 -15 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 4.E-05 -15 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 TC B total vorticity TC C total vorticity 8.00E-05 7.50E-05 7.50E-05 7.00E-05 7.00E-05 6.50E-05 6.50E-05 6.00E-05 6.00E-05 5.50E-05 5.50E-05 5.00E-05 5.00E-05 4.50E-05 4.50E-05 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 TC D total vorticity TC E total vorticity 1.00E-04 9.50E-05 9.00E-05 9.00E-05 8.50E-05 8.00E-05 8.00E-05 7.50E-05 7.00E-05 7.00E-05 6.50E-05 6.00E-05 6.00E-05 5.00E-05 5.50E-05 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1
V k = + + + + + + + ( ) ( ) ( ) ( ) V f C f f V R B t p p p Tendency term Advection term Divergence term Tilting term Residual term Tendency Advection Divergence Tilting term Residual term ( V V ( ) ) V C = + + ( ) k R B p t p TC A 7.01 -15.50 25.40 -1.29 -1.60 0 -15 TC B 15.40 -12.62 9.02 -7.26 26.26 0 -9 TC C 7.50 -12.20 7.51 -5.26 17.45 +1 -10 TC D 20.34 2.08 23.39 -3.08 -2.05 0 -9 TC E 10.49 -4.13 13.38 -0.11 1.35 0 -12
TC A TC B TC C TC D TC E TC A total vorticity 1.E-04 8.50E-05 9.E-05 8.00E-05 8.E-05 7.50E-05 7.00E-05 7.E-05 6.50E-05 6.E-05 6.00E-05 5.E-05 5.50E-05 4.E-05 -15 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 -15 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 TC B total vorticity TC C total vorticity 8.00E-05 7.50E-05 7.50E-05 7.00E-05 7.00E-05 6.50E-05 6.50E-05 6.00E-05 6.00E-05 5.50E-05 5.50E-05 5.00E-05 5.00E-05 4.50E-05 4.50E-05 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 TC D total vorticity TC E total vorticity 1.00E-04 9.50E-05 9.00E-05 9.00E-05 8.50E-05 8.00E-05 8.00E-05 7.50E-05 7.00E-05 7.00E-05 6.50E-05 6.00E-05 6.00E-05 5.00E-05 5.50E-05 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1
V k = + + + + + + + ( ) ( ) ( ) ( ) V f C f f V R B t p p p Tendency term Advection term Divergence term Tilting term Residual term Tendency Advection Divergence Tilting term Residual term ( V V ( ) ) V C = + + ( ) k R B p t p TC A TC B TC C TC D TC E * 22.44 30.26 17.54 76.88 26.39 1.97 -15.06 -20.38 -18.56 -4.90 2.64 -0.42 19.41 14.48 9.27 29.01 10.70 5.33 -5.89 -8.52 -7.90 -7.16 -1.96 -2.82 23.98 44.68 34.72 59.93 15.00 -0.12 -3 -6 0 -4 -3 -8 -6 -8 -4 -8 *an anti-cyclone case is calculated to check the calculation is correct.
V k = + + + + + ) + + ( ) ( ) ( ( ) V f C f f V R B t p p p Tendency term Advection term Divergence term Tilting term Residual term + ( ) D f V k = + + + = + ) + + V ( ) ( ) ( ) ( ( ) C f f V R B Dt t p p + = + + + Considering ( ) ( ' ) ( ) ' f V f V V = + + + + + ( ) ( ) ' ' ' ' f V f V V V = + , ' A A A + D1 D2 D3 DD = + A A + A A cli A IAV + ISV ' ' V V V V V = + + ' + ( ) ' k k MRGTD A p p p p p ER T1 T2 T3 TD You may check the following speculations ( + ) D f 1. D1+T1 Dt D ' 2. D2+D3+T2+T3 +DD+TD+R Dt Balanced dynamics Aggregate by convective vortices
Wave Dynamics ( + ( + t ) ) D f f D1+T1 (D1) difference Dt 2.75 3.01 9.45 24.20 11.30 (4.48) (4.01) (1.00) (8.44) (6.33) 3.15 3.04 8.35 25.08 10.42 (4.85) (3.70) (8.53) (23.92) (10.83) -0.40 -0.03 1.10 -0.88 0.88 TC A TC B TC C TC D TC E TC A Balanced TC B Agg TC C Agg D ' D2+D3+T2+T3 +DD+TD+R Dt Aggregate by convective vortices Eddy vorticity tendency Balanced dynamics TC D Wave D2+D3+ T2+T3 15.35 1.80 5.43 9.83 5.49 ' ' D (D2+D3) DD+TD+R (R) Dt t 19.76 25.01 10.26 -5.94 3.33 (2.53) (11.39) (6.50) (11.90) (4.16) 4.41 23.21 4.83 -15.78 -2.16 (-1.60) (26.26) (17.45) (-2.05) (1.35) (11.54) (4.55) (7.14) (7.50) (4.92) TC A TC B TC C TC D TC E TC E
Next: 1. Explain the contributions of each term in vorticity budget for each TC formation, 2. Describe the behavior of waves when wave dynamic or balance dynamic is important, 3. Compare the results of vorticity budget with our past observation analysis.
an anti-cyclone case is calculated to check the calculation is correct. V k = + + + + + + + ( ) ( ) ( ) ( ) V f C f f V R B t p p p Tend ADVh ADVv ADVc DIV Tilting Residual 1.97 -2.80 -0.93 3.31 5.33 -2.82 -0.12