Comparing and Ordering Fractions with Different Denominators
Learn how to compare and order fractions with different denominators to determine which is greater. Understand the concept of finding a common denominator, multiplying fractions to make denominators the same, and comparing numerators to find the larger fraction. Explore examples and practice exercises to enhance your understanding of fractions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
02 March 2025 Where are we in our learning journey? Comparing and ordering fractions (different denominators) WALT Learning Outcomes: Which is the bigger fraction? 5 7 or 3 5 Put the following fractions in ascending order? 1 6 , 2 5 12 , 1 4 , 18 3 , Keyword(s) Parts Whole Numerator Denominator 24
RECAP Compare these fractions, using <, > or = 7 3 > 16 16 11 20 11 18 >
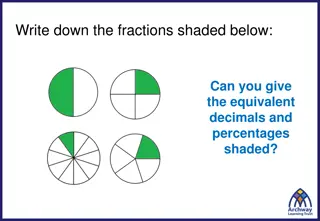
EXPLORE Which diagram doesn t have a pair? 2 3 4 5 3 4 3 4 4 5
QUESTION Compare these fractions, using <, > or = Can you explain why and fill in the blank? 2 6 5 6 6 8 5 < > 12 How can we compare fractions without using a diagram?
DEFINE Fractions can be compared more easily by making the denominators the same. Find the common denominator Multiply fractions to make the denominators the same Compare the numerators. If the numerator is bigger then the fraction is bigger.
EXAMPLE Compare these fractions Common denominator 8 and 12 both go into 24 3 8 5 > 12 Make denominators the same 8 needs to be multiplied by 3 ? ? ? ? 10 24 9 24 > 12 needs to be multiplied by 2 Compare numerators 10 is bigger than 9 therefore 5/12 is bigger than 3/8
EXAMPLE Compare these fractions Common denominator 9 and 6 both go into 18 8 9 5 6 > Make denominators the same 9 needs to be multiplied by 2 ? ? ? ? 15 18 16 18 > 6 needs to be multiplied by 3 Compare numerators 16 is bigger than 15 therefore 8/9 is bigger than 5/6
CHECK 3 4 5 6 > ? ? ? ? 10 12 9 > 12
CHECK 3 7 1 3 > ? ? ? ? 7 9 > 21 21
DEFINE Fractions can also be compared by putting them in order. Ascending means from smallest to biggest. Descending means from biggest to smallest.
EXAMPLE Put the following fractions in ascending order: The common denominator is 24. 7 3 4 5 8 4 6 12 Each fraction needs to then be converted so that all the denominators are the same. ? ? ? ? ? ? ? ? 14 24 18 24 16 24 15 24 The numerators can then be compared. 7 3 4 5 8 4 6 > > > 12
EXAMPLE Put the following fractions in descending order: The common denominator is 18. 2 9 1 3 1 6 1 18 ? 1 Each fraction needs to then be converted so that all the denominators are the same. ? ? ? ? ? 4 18 3 6 19 18 18 18 The numerators can then be compared. 1 18> 1 6 1 3 2 9 > > 1
EXERCISE Put the following fractions in ascending order:
EXIT TICKET Put the following fractions in descending order: 6 8 4 6 10 12 19 24 13 16 32 48 39 48 38 48 40 48 36 48 6 8 4 6 19 24 10 12 13 16 > > > >
REFLECTION What have you learnt today? . I fully understand I don t understand I need more practice! What Went Well? Even Better If? Think about how you can improve your learning