Computational Approach to Percolation Theory & Forest Fires
Explore the fascinating realm of percolation theory, which delves into connected clusters in random lattices as probabilities increase. Discover how this theory not only models fluid flows in porous materials but also aids in understanding critical thresholds, such as the percolation threshold. Delve into the intriguing application of percolation theory in modeling phase transitions, as exemplified by the forest fire model on discrete lattices.
Uploaded on | 0 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
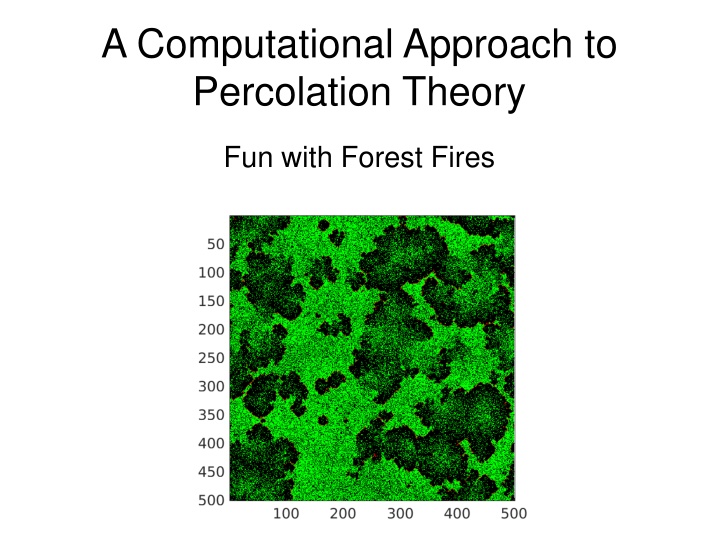
A Computational Approach to Percolation Theory Fun with Forest Fires IA
Percolation Percolation theory is a problem in math and physics concerning the size of connected clusters in a random lattice as the probability of their components increases As the name suggests, part of the motivation is modeling the flow of fluids through porous materials. But it can also model other things.
Percolation One interesting problem in percolation is that of the critical threshold or the percolation threshold which refers to the required probability to create a cluster that has infinite connectivity on an infinite lattice (site percolation). This is dependent on the structure of the lattice. A one-dimensional lattice clearly has a threshold of 1, while a 2d square lattice has a threshold of ~0.59.
Percolation This becomes useful for modeling phase transitions One example is the forest fire model. Some starting assumptions: Forests can be modeled as discrete lattices Lattice sites can be empty, on fire, or containing a tree Trees might appear in empty spots and fire might appear in spots with trees Fires spread to adjacent sites
Percolation This becomes useful for modeling phase transitions One example is the forest fire model. Some starting assumptions: Forests can be modeled as discrete lattices Lattice sites can be empty, on fire, or containing a tree Trees might appear in empty spots and fire might appear in spots with trees Fires spread to adjacent sites
Sources Christensen, Kim. "Percolation theory." Imperial College London, London (2002): 40. Christensen, Kim, Henrik Flyvbjerg, and Zeev Olami. "Self-organized critical forest-fire model: Mean-field theory and simulation results in 1 to 6 dimenisons." Physical review letters 71.17 (1993): 2737.






















