Connected Particles and Friction
System analysis of connected particles with friction and tension. Calculating acceleration, tensions in strings using forces and equations. Detailed step-by-step solution provided.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
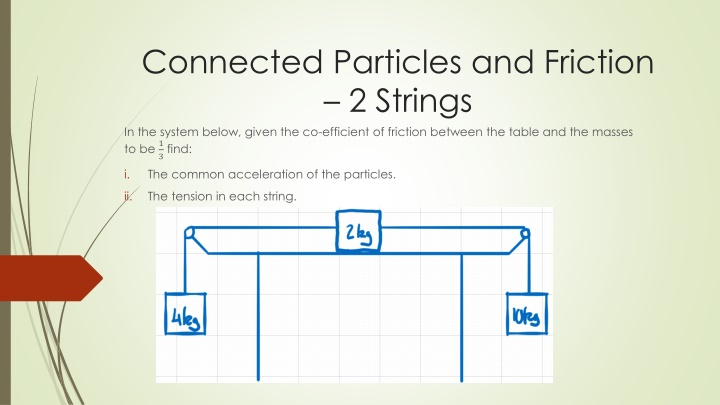
Connected Particles and Friction 2 Strings In the system below, given the co-efficient of friction between the table and the masses to be 1 3find: The common acceleration of the particles. i. ii. The tension in each string.
As we have seen previously we need to begin these questions by considering the forces that act on each particle. Remember, it is an imbalance of forces causes movement in a specific direction. We should also note that each string will have its own tension. However, the system will have one acceleration throughout. Here are the forces acting on the 4kg particle: Assuming there is an imbalance of forces upwards (T is larger than 4g), using ? = ?? we get: ? 4? = 4? .(??1)
Here are the forces acting on the 2kg particle: As there is no upward or downward movement, we know ? = 2?. This allows us to calculate friction: ? = ?? ? =1 3(2?) ? =2? 3 Assuming movement to the right, we get: ? ? 2? 3= 2? .(??2)
Here are the forces acting on the 10kg particle: As 10g is a greater force than S, we get: 10? ? = 10? (??3) We now need to consider how to solve this system of equations. It can be helpful to eliminate T from ??1, eliminate S from ??3and substitute these into ??2: From ??1: ? = 4? + 4? From ??3: ? = 10? 10? Filling into ??2we get: 10? 10? 4? + 4? 2? 3= 2?.
30? 30? 12? 12? 2? = 6? 30? 12? 2? = 6? + 12? + 30? 16? = 48? 16? 48= ? ? 3?? 2= ? We can use this value of ? to find ? and ?: ? = 4? + 4? ? = 10? 10? ? 3+ 4? ? = 10? 10(? ? = 4 3) ? =4?+12? ? =30? 10? 3 3 ? =16? ? =20? 3N 3N