Construction of Plane Figures: Projections and True Size
Construction of the true size of plane figures through horizontal/vertical profile projecting planes including projection of a circle, determination of the true size of a triangle, and construction exercises involving squares, circles, and other figures.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
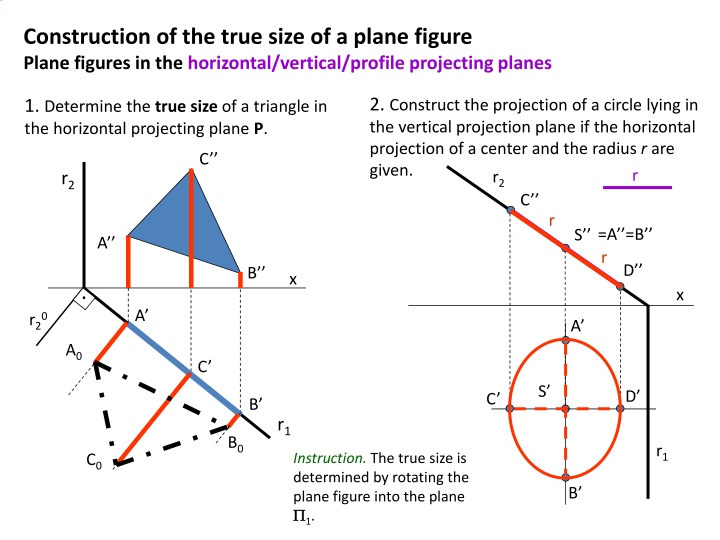
Construction of the true size of a plane figure Plane figures in the horizontal/vertical/profile projecting planes 2. Construct the projection of a circle lying in the vertical projection plane if the horizontal projection of a center and the radius r are given. r2 C 1. Determine the true size of a triangle in the horizontal projecting plane P. C r r2 r =A =B S A r D B x . x A r20 A A0 C S D C B r1 B0 r1 Instruction. The true size is determined by rotating the plane figure into the plane 1. C0 B
Revolution of a point about the 1st trace of the plane into the plane 1. r2 S Remark. The revolution about the 2nd trace into the plane 2 is analoguous. x (S*) t S t0 T1 S0 (S) r1
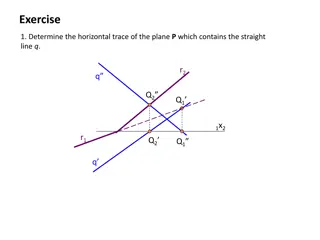
Exercises. s2 1. Construct the projections of a square whose one side lies on the line p, and one vertice is the point A. p q D A C Instruction. a) (p, q) = (using two parallel lines) b) Rotate the point A into 1. c) p || q (p) || (q) x B D p C q A d) (A)(B)(C)(D) one of the two solutions e) Using afinity A0 B A B C D (B) (C) f) Lines of recall s1 A B C D (D) (A) (q) Remark. Projection of a square is always a parallelogram. (p)
2. Plane is determined with the traces s1and s2. Construct the projection of the circle k whose center id the point S, and the radius is r. s2 S0 r S k Projection of a circle is an ellipse for which the axes have to be determined. REMARK! x k In every projection the major axis is on the apropriate principal line, and the minor axis is on apropriate the steepest line (the lenght of the minor axis is determined with the rotated steepest line). Horizontal projection of the major and minor axis is projected into the conjugated diameters of the elipse in the vertical projecting plane. r S r S0 r r s1
C r2 Exercises. A 1. Construct the true size of the triangle ABC. B Instruction. C a) Construct the traces of the triangle plane determined by two intersecting lines. b) Rotate the point A into 1. A B A0 (B) c) Construct the point (B) and (C) with the afinity (axis r1). r1 (A) (C)
C0 B0 2. Construct the projection of a regular hexagon lying in the plane , whose longer diagonal is the line segment AD. D0 z S0 B B A0 s2 A C A E0 S F0 S F D D F B E E A C s3 S D F E s1 y