Constructive Dismissal Masterclass Overview
Constructive dismissal is defined as an employee resigning due to their employer's conduct breaching the contract. This masterclass covers key aspects such as the implied duty of trust, financial implications, responding to claims, defense strategies, grey areas, and practical tips.
Uploaded on Apr 13, 2025 | 0 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
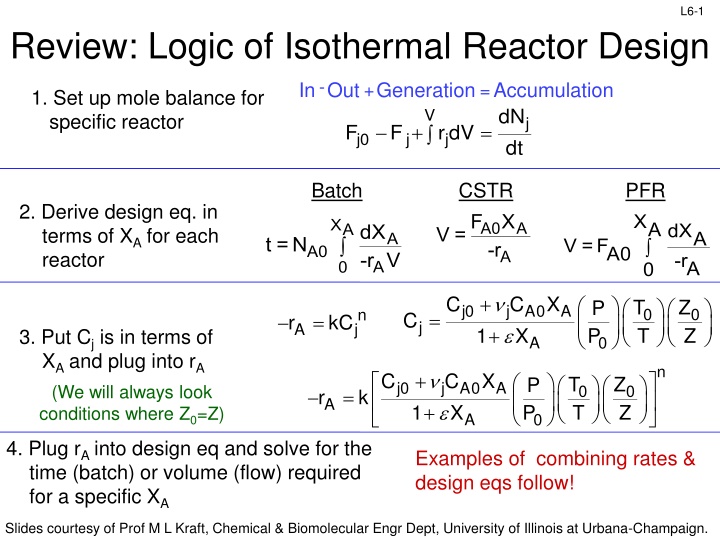
L6-1 Review: Logic of Isothermal Reactor Design In Out - +Generation =Accumulation 1. Set up mole balance for specific reactor dN dt V j + = F F rdV j0 j j Batch CSTR PFR 2. Derive design eq. in terms of XA for each reactor F X XA dXA 0 XA A0 -r A dX -r V V = A t =N V =FA0 0 A0 A -rA A + + C C X T T Z Z P P j0 A0 X j A 0 0 n j = C = r kC j A 1 3. Put Cj is in terms of XA and plug into rA (We will always look conditions where Z0=Z) A 0 n + + C C X T T Z Z P P j0 A0 X j A 0 0 = r k A 1 A 0 4. Plug rA into design eq and solve for the time (batch) or volume (flow) required for a specific XA Examples of combining rates & design eqs follow! Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-2 Review: Batch Reactor Operation A B -rA = kCA2 2nd order reaction rate Calculate the time required for a conversion of XA in a constant V batch reactor dX dt Be able to do these 4 steps, and A = r N V then integrate to solve for time Mole balance A0 A 2 = Rate law Ar kC for ANY REACTION A = (1 X ) Stoichiometry (put CA in terms of X) C C A A0 A ( )( d X 2 ) 2 A = N k C 1 X V Combine A0 A 0 A dt Batch Volume is constant, V=V0 ( A0 t d 1 kC 1 X )( dX Integrate this equation in order to solve for time, t 2 ) 2 A = N k C 1 X V A0 A 0 X A = t A0 A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-3 Review: CSTR Operation A B -rA = kCA Calculate the CSTR volume required to get a conversion of XA 1st order reaction rate F X A 0 A = V Mole balance r A = r kC Rate law A A = (1 X ) Stoichiometry (put CA in terms of X) C C A A0 A F X Put FA0 in terms of CA0 A0 1 X = V ( ) Combine kC A0 A Volume required to achieve XA for 1st order rxn A0 0 C X X A 0 A = = V V ( ) ( ) kC 1 X k 1 X A0 A A Be able to do these steps for any order reaction! Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-4 Review: Scaling CSTRs If one knows the volume of the pilot-scale reactor required to achieve XA, how is this information used to achieve XA in a larger reactor? Suppose for a 1st order irreversible rxn: X X 0 A 0 A = = known: V want: V small bigger ( ) ( ) k 1 X k 1 X A A Want XA in the small reactor to be the same as XA in the bigger reactor k in the small reactor is the same as k in the bigger reactor 0 in the small reactor must be different from 0 in the bigger reactor So the reactor volume must be proportional to the volumetric flow rate 0 X V X Separate variables we will vary from those held constant A 0 A = = V ( ) ( ) k 1 X k 1 X 0 A A Eq is for a 1st order rxn only! Space time (residence time) required to achieve XA for 1st order irreversible rxn Be able to do this for any order rxn! X A = = V ( ) 0 k 1 X A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-5 Review: Damk hler Number, Da r V rate of reaction Da F enterin g flow rate of A at en trance reaction rate convection rat A0 = = = e A0 Estimates the degree of conversion that can be obtained in a flow reactor First order irreversible reaction: r Da F 1st order irreversible reaction V k C C V kV A0 A0 = = = Da = k Da A0 0 0 A0 = V Substitute 0 Second order irreversible reaction: 2nd order irreversible reaction 2 kC V A0 r F V kC C V A 0 A0 = = = = Da D a Da kC A0 A0 0 0 A 0 How is XA related to Da in a first order irreversible reaction in a flow reactor? Da X 1 Da + slide L6-7: + If Da < 0.1, then XA < 0.1 If Da > 10, then XA > 0.9 k From = = X A A 1 k Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-6 Review: Sizing CSTRs for 2nd Order Rxn A B -rA = kCA2 Liquid-phase 2nd order reaction rate Calculate the CSTR volume required to get a conversion of XA F X C X A0 r 0 A0 r = = V Mole balance A A 2 = Ar kC Rate laws A Be able to do these steps! = (1 X) C C Stoichiometry A A0 In terms of space time? C X V X 0 A0 1 = = = V Combine or 2 2 ( ) 2 ( ) kC X kC 1 X 0 A 0 A 0 ( ) 1 2 kC + 1 4 kC + A0 2 kC A0 = X In terms of conversion? A0 Eq is for a 2nd order liquid irreversible rxn ( ) 2Da In terms of XA as a function of Da? 1 2Da + 1 4Da + = X = Da kC A0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-7 Review: n CSTRs in Series CA0 0 CA1 = CA2 1st order irreversible liquid-phase rxn run in n CSTRs with identical V, and k C + A0 = C For n identical CSTRs, then: An n ( ) 1 k Rate of disappearance of A in the nth reactor: C + A0 An r = = kC k An n ( ) 1 k How is conversion related to the # of CSTRs in series? Put CAn in terms of XA (XA at the last CSTR): 1 C + ( ) A0 = 1 X = 1 X C A A0 A n n ( ) ( ) + 1 k 1 k 1st order irreversible liquid phase rxn run in n CSTRs with identical V, and k 1 1 = = 1 X or 1 X A A n n ( ) ( ) + 1 Da + 1 k Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-8 Review: Isothermal CSTRs in Parallel Mole Balance FA01 X Subscript i denotes reactor i Ai r = V A0i F FA0 i Ai FA02 same T, V, FA01 = FA02= FA0n X A r = V F X = X =...= X = X r r = A0 1 2 n A = = = ... An r r A1 A2 A total volume of all CSTRs # of CSTRs Volume of each CSTR V n = = V i F X V n A0 n Ai r = Ai F total molar flow rate # of CSTRs A0 n = = A0i F X A r = V F Molar flow rate of each CSTR A0 A Conversion achieved by any one of the reactors in parallel is the same as if all the reactant were fed into one big reactor of volume V Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-9 Liquid Phase Reaction in PFR LIQUID PHASE: Ci f(P) no pressure drop 2A B -rA = kCA22nd order reaction rate Calculate volume required to get a conversion of XA in a PFR integrate & solve for V for ANY F d X dV r Be able to do these 4 steps, A A = Mole balance A0 2 = Rate law r kC A A ORDER RXN Stoichiometry (put CA in terms of X) = C C (1 X ) A A0 ( A )( F 2 ) 2 k C 1 X d X d A0 A A = Combine V A0 X V F X F dX A A0 A A0 A = = V dV ( ) ( ) 2 2 1 X 2 ( ) k C k C 1 X A 0 0 A0 A0 A See Appendix A for integrals frequently used in reactor design Liquid-phase 2nd order reaction in PFR Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-10 Liquid Phase Reaction in PBR LIQUID PHASE: Ci f(P) no pressure drop 2A B -r A = kCA22nd order reaction rate Calculate catalyst weight required to get a conversion of XA in a PBR Be able to do these 4 steps, integrate F d dW X r ' & solve for V for ANY ORDER RXN A A = Mole balance A0 2 = Rate law r' kC A A Stoichiometry (put CA in terms of X) = C C (1 X ) A A0 ( A )( F 2 ) 2 k C 1 X d X W d A0 A A = Combine A0 X F X W F dX A A0 A A0 = A W = dW ( ) 0 0 ( ) 2 1 X 2 2 ( ) k C k C 1 X A A0 A0 A Liquid-phase 2nd order reaction in PBR Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-11 Isobaric, Isothermal, Ideal Rxns in Tubular Reactors Gas-phase reactions are usually carried out in tubular reactors (PFRs & PBRs) Plug flow: no radial variations in concentration, temperature, & -rA No stirring element, so flow must be turbulent FA0 FA + + + + C C X C C X 1 1 T T Z Z P P j0 A0 X j A j0 A0 X j A 0 0 = = C C GAS PHASE: j j 1 1 A A 0 1 Stoichiometry for basis species A: ( ) + C 1 X X C C X A0 1 A A0 A0 X A = = C C A A + 1 A A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-12 Isobaric, Isothermal, Ideal Rxn in PFR GAS PHASE: Ci = f( ) no P, T, or Z 2A B -rA = kCA22nd order reaction rate Calculate PFR volume required to get a conversion of XA F d X dV r A A = Mole balance A0 2 = Rate law Ar kC A 1 X X + ( ) C A0 1 A Stoichiometry (put CA in terms of X) = C A A 2 2 ( ) ( X ) 1 X k C dX d A0 + A A = Combine 2 ( ) V 1 F A A 0 2 ( ) 2 XA + 1 X F A A0 = V dX Integral A-7 in appendix ( ) A 2 ( ) 1 X k C 0 A0 A )2 ( Gas-phase 2nd order rxn in PFR no P, T, or Z + 1 X F ( ) ( ln 1 X ) 2 A A0 = + + + V 2 1 X ( ) A A 1 X 2 k C A A0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-13 Effect of on and XA Tf T0 N N Change in total # moles at X N = 1 A = = total moles fed T0 : expansion factor, the fraction of change in V per mol A reacted 0: volumetric flow rate varies if gas phase & moles product moles reactant, or if a P, T, or Z occurs No P, T, or Z occurs, but moles product moles reactant = = 0 (mol product = mol reactants): = : constant volumetric flow rate as XA increases < 0 (mol product < mol reactants): volumetric flow rate decreases as XA increases Longer residence time than when = Higher conversion per volume of reactor (weight of catalyst) than if = 0 > 0 (mol product > mol reactants): with increasing XA Shorter residence time than when = Lower conversion per volume of reactor (weight of catalyst) than if = 0 P P Z Z T T ( ) 0 = + 1 X 0 A 0 0 ( ) + 1 X 0 A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-14 Pressure Drop in PFRs & PBRs + + C C X Considering ideal gas phase behavior (Z0=Z) T T P P j0 A0 X j A 0 = C GAS PHASE: j 1 A 0 Concentration is a function of P so pressure drop is important in gas phase rxns Take a 1st order reaction A B in a PBR with r A = kCA Why? + C C X T T P P Substitute concentration of A into the rate law: A0 A0 X A 0 = r ' k A 1 A 0 If P drops during the reaction, P/P0 is less than one, so CA & the rxn rate Use the differential forms of the design equations to address pressure drop PFR PBR For tubular reactors: dX dV moles dm dX dW moles A = F r A = F r' ( )( A0 A A0 A ( )( ) ) 3 g catalyst min min Pressure drops are especially common in reactions run in PBRs we will focus on PBR applications Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-15 Pressure Drop in PBRs GAS PHASE: A B -r A = kCA2 Calculate dXA/dW for an isothermal ideal gas phase reaction with P 2nd order reaction rate dX d = A = F r' Mole balance A0 A W kC 2 Rate law r' A A ( ) X C 1 X ) ( ( 1 P P A0 1 A = C Stoichiometry (put CA in terms of X) A + A 0 ( 2 2 2 k C ) Combine 1 X dX dW P P A0 A A = 2 ) F + X A0 0 A This eq. is solved simultaneously with an eq. that describes how the pressure drops as the reactant moves down the reactor 2 2 ( 1 ) 1 X + kC dX dW P P A A0 A = 2 ( ) X 0 0 A Function of XA and pressure We need to relate P/P0 to W Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-16 Ergun Equation relates P to W P dP dW T )( ) 0 = + 1 X This equation can be simplified to: A ( 2 T P P 0 0 dy dW T T Differential form of Ergun equation for pressure drop in PBR: ( ) = + 1 X A 2y 0 N N 2 P P Tf T0 0 = = = = y y A0 ( ) c c N A 1 P 0 T0 0 volume of solid ( ) 1 : fraction of solid in bed =total bed volume C: particle density AC: cross-sectional area : constant for each reactor, calculated using a complex equation that depends on properties of bed (gas density, particle size, gas viscosity, void volume in bed, etc) : constant dependant on the packing in the bed Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-17 Gas Phase Reaction in PBR with P GAS PHASE: A B -r A = kCA2 Calculate dXA/dW for an isothermal ideal gas phase reaction with P 2nd order reaction rate dX d A = F r' Mole balance A0 A W 2 2 ( 1 ) 1 X k C dX dW P P Combine with rate law and stoichiometry A A0 A = 2 ( ) + X 0 0 A P Relate P/P0 to W dP dW T )( ) 0 = + 1 X A ( 2 T P P 0 0 Ergun Equation can be simplified by using y=P/P0 and T=T0: dy dW ( ) = + 1 X A 2y Simultaneously solve dXA/dW and dP/dW (or dy/dW) using Polymath Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-18 Analytical Solutions to P/P0 Sometimes P/P0 can be calculated analytically. When T is constant and = 0: dy dW dy dW T ( ) = = + 1 X 0 1 Evaluate A 2y 2y T 0 1 To pressure change P P = y W P P0 1 0 2 = y W = = 2ydy dW 2ydy dW 0 P P0 = 1 From no pressure change 2 P P Only for isothermal rxn where =0 P P = 1 W = 1 W 0 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-19 Pressure Drop Example GAS PHASE: A B This gas phase reaction is carried out isothermally in a PBR. Relate the catalyst weight to XA = A0 F d W -r A = kCA2 2nd order reaction rate N N dX 1 1 1 Tf T0 A = = = 0 r' A N T0 + C C X T T P P ) P P A0 A0 X 0 A 0 ( = C = C C 1 X A A A0 A 1 A 0 0 1 P P Plug into CA = = 1 W = 0 and isothermal, so: C C C X 1 W A A0 A0 A 0 Plug into PBR design eq: dX dW dX dW ( ) 2 ( ) 2 A A = = F k C F k C 1 X 1 W A0 A A 0 A0 A Simplify, integrate, and solve for XA in terms of W or W in terms of XA: X W F dX A dX dW ( ) A0 A 2 ( ) ( ) 2 = W dW A 1 = 0 0 F kC 1 X 1 W A0 A0 A 2 2 ( ) kC 1 X A0 A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-20 Pressure Drop Example A B -r A = kCA2 2nd order gas phase rxn non-elementary rate This gas phase reaction is carried out isothermally in a PBR. Relate the catalyst weight to XA ( ) = 0 0 A A0 k X C 1 A 1 X = 0 2 + 0 2 = + 0 2 X W X W 2 F dX A A0 C A X A0 A = W 1 W d 1 W k 1 2 2 ( ) A0 A W 2 kC kC X W 2 W 2 A0 A = W 1 Solve for XA 0 kC W A0 A0 X W 1 W 1 X A A 0 kC kC W A0 A0 = X W 1 X W 1 A A 0 kC W 2 A0 1 2 kC X 0 X 0 A 1 1 A Rearrange eq. for W: kC W 1 X A0 1 1 A0 A = W Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L6-21 Next Time Startup of a CSTR under isothermal conditions Semi-batch reactor Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.