Crystal Symmetry in Reciprocal Space: Periodic Functions and Lattices
Explore the fascinating world of crystal symmetry in reciprocal space, diving into topics such as periodic functions on lattices, the Bravais lattice's total symmetry, and the relationships between real space and reciprocal space. Discover the intricacies of the reciprocal lattice, primitive lattice, Fourier series, and more in this comprehensive guide.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
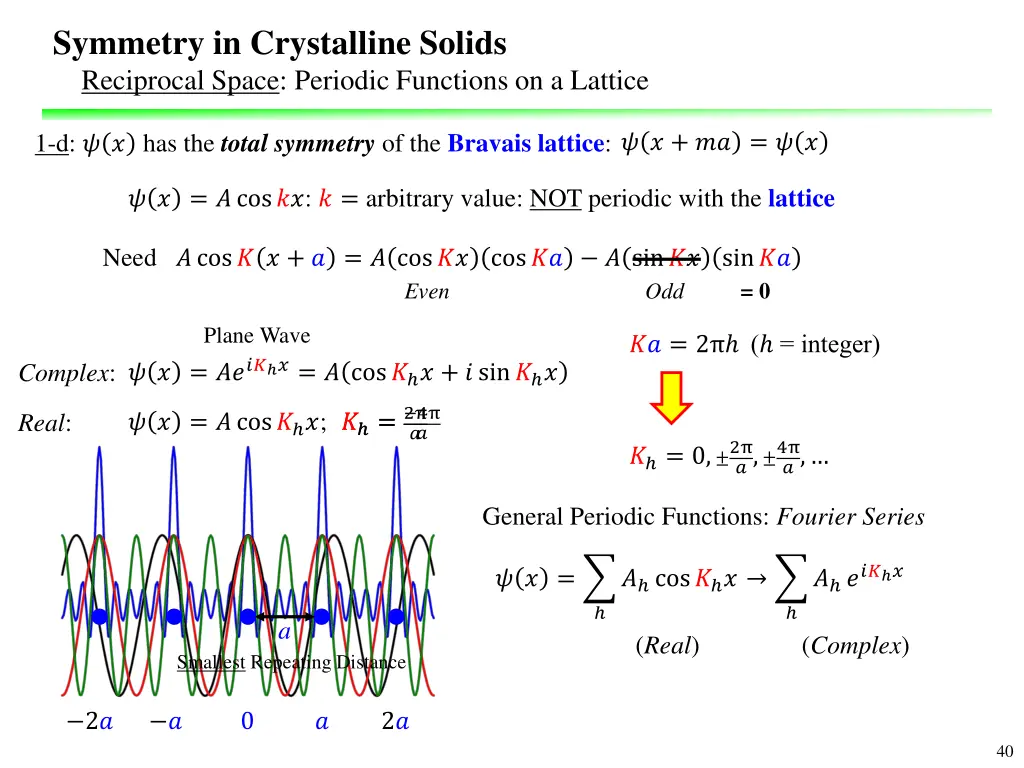
Symmetry in Crystalline Solids Reciprocal Space: Periodic Functions on a Lattice 1-d: ? ? has the total symmetryof the Bravais lattice: ? ? + ?? = ? ? : NOT periodic with the lattice ? ? = ?cos??: ? = arbitrary value Need ?cos? ? + ? = ? cos?? cos?? ? sin?? sin?? Need ?cos? ? + ? = ? cos?? Even = 0 Odd Plane Wave ?? = 2 ( = integer) ? ? = ???? ?= ? cos? ? + ? sin? ? ? ? = ???? ? Complex: ? =2 ? = 4 ? ? = ?cos? ?; Real: ? ? ? = 0, 2 ?, 4 ?, General Periodic Functions: Fourier Series ? ??? ? ? ? = ? ? = ? cos? ? ? cos? ? a (Real) (Complex) Smallest Repeating Distance 2? ? 0 ? 2? 40
Franzen, Ch. 4 Symmetry in Crystalline Solids Reciprocal Space: The Reciprocal Lattice ? ? + ???? = ? ? = ???? ?? ? ? ? + ???? = ? ? 3-d: ? ? has the total symmetryof the Bravais lattice: ???? ?? ?+????= ???? ?? ? ??? ?? ???? ???? ?? ?+????= ???? ?? ? Primitive Lattice = 1 ????= ??1+ ??2+??3 ?,?,? integers ? ?? ?1= 2 Reciprocal Lattice + ??2 + ??3 ,?,? integers = 2 ??? ? ??= ?1 ?? ?? ? ?? ?2= 2 ? ? ?? ?3= 2 ? ?,? = 1,2,3 ? ? = ???? ? Complex: ? =2 ? ? = ?cos? ?; Real: ? ? = 0, 2 ? = 0, 2 ? = 0, 2 ?, 4 ?, = 2 ?, 4 ?, = 2 ?, 4 = ? ?, ? ? : ? : ?? Reciprocal (Space) Lattice Set of all wavevectors that yield plane waves with periodicity of Bravais lattice Bravais ( Real Space ) Lattice a 2 ? 22 2 22 2 ? ? 0 ? ? ? 2? ? 0 ? 2? 2? ? 2? 0 41
Franzen, Ch. 4 Symmetry in Crystalline Solids Reciprocal Space: The Reciprocal Lattice Bravais Lattice: ????= ??1+ ??2+??3 ?,?,? integers Reciprocal Lattice: ? ??= ?1 Primitive Lattice ?1= Volume of Unit Cell + ??2 + ??3 ,?,? integers 2? ?1 2? ?1 2? ?1 = 2 ???: = = = ?1 ?2 ?3 ?2 ?3 ?1 ?3 ?1 ?2 ?? ?? ?2 and ?3 ?3 and ?1 ?1 and ?2 Example: Hexagonal lattice, looking down ? = ?3: Real Space: ?1= ?2= ? 3= 120 Reciprocal Space: ?1 3 4 3? = ?2 = 60 = ?00 ?00 ?1 ?2 Same Rotational Symmetry ?1 ?2 ?10 ?01 ?2 ?1 ?1 ?2 ?10 ?01 Relationships between Real Space and Reciprocal Space 3-d Lattices: Primitive Base-Centered Primitive Base-Centered Body-Centered Face-Centered Face-Centered Body-Centered 42
Franzen, Ch. 5 Symmetry in Crystalline Solids Reciprocal Space: Irreducible Representations of the Translation Group (1-d) Real Space: ???? = ? ??? ?? ? ? = 1,2,3,4: Label of IR ? = 1,2,3,4: Label of Class Periodic Boundary Conditions Unit Cell Bravais Lattice: ?1= 1 ? ?2= 1 2? = ?1,?2,?3,?4= ?0 AbelianGroup Identity ?3= 1 3? 4 Classes ?4= 1 4? 1 ? = ?0 Irreducible Representations: ?1,?2,?3,?4 1-dimensional: complex numbers 4= 1 ?4= = 1 4? = ?4= = ?0 Let ???1 = ? ?1 1= ? 3= +? 2= 1 4= +1 4= ? 4= ? 4 2??? 4 4= ???1 ???1 ???1 ???1 4= ???1 4= ???1 4= ???1 4= 1: 4 ?= ? 4= ???0 = 1 ???1 ?= ? ?= ? ? ? ??= 1 ?? = 1 ??= ?1 ??= 1 ?? ? ???? = ???1 ???? = ???1 ???? = ???1 ???? = ???1 ???? ?= ???1 ?= ???1 ?= ? 2???? 4 ?= ???1 ? Vector Notation 2????? 4? 4? 4? 4 4? 2????? 2????? 2???? 2????? 2?? 2?? 2?? 4? 4? 4? ? ? 4 4 2? 2? ? ? = ? = ? = ? ?? = ? ?? = ? ?? ?? = ??? ?? ?? Wavevector ?? ?? 43
Franzen, Ch. 5 Symmetry in Crystalline Solids Reciprocal Space: Irreducible Representations of the Translation Group (1-d) Real Space: Reciprocal Space: 2? ? ? 2 2 ? 0 ? ?4= ?0 Character Table: ??=? 2? ? ?? ???? = ? ??? ?? ???? ???? = ? ??? ??= ? ???? = ? ??? ?? 2??? 4 4 Classes Real Imaginary Features of Basis Functions ?? ?? ?? ?? ?? IRs ??=?? ??= 0: +1 +1 +1 +1 Totally Symmetric ?4 ?0 ?: Complex Conjugate of ?3 ??=? +1 1 +i i ?1 ??: ??=? +1 1 +1 1 ?2 ?: Complex Conjugate of ?1 ??=?? +1 +i 1 i ?3 ??: Identity (Periodic Boundary Conditions) 44
Franzen, Ch. 5 Symmetry in Crystalline Solids Reciprocal Space: Irreducible Representations of the Translation Group (1-d) (3-d) Real Space: Reciprocal Space: ?1= 8 ?1= 16 2? ? ? 2 2 ? 0 ? = ?1,?2, ,??1= ?0 ? ? ? What are the basis functions for these IRs? ??? = ? ??? ??= ? 2??? ?1 2? ? ? ? ?1 ?1 ? 2? ?= ? ?1 As ?1 , the set of wavevectors ??becomes continuous As ?1 ??is a quasi -continuous space: Reciprocal Space ??= ??= ? = 0,1,2, , ?1 1 (Momentum Space) + ??2 + ??3 = ????= ??1+ ??2+ ??3 = ? ??= ?1 ? = 0,1,2, , ?1 1 ? = 0,1,2, , ?2 1 ? = 0,1,2, , ?3 1 Periodic Boundary Conditions ???? ???? = ? ????? ???? ? = 0,1,2, , ?1 1 ? = 0,1,2, , ?2 1 ? = 0,1,2, , ?3 1 ? ?1 ? ? ?3 + + ????= ?1 ?2 ?3 ?2 45
