Crystal Systems Unit Cell: Smallest Repetitive Volume with Lattice Pattern
Unit cell plays a crucial role in defining crystal structures and systems, showcasing the intricate atomic arrangements within. Explore crystallographic directions, indices determination, and more within the realm of crystallography.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
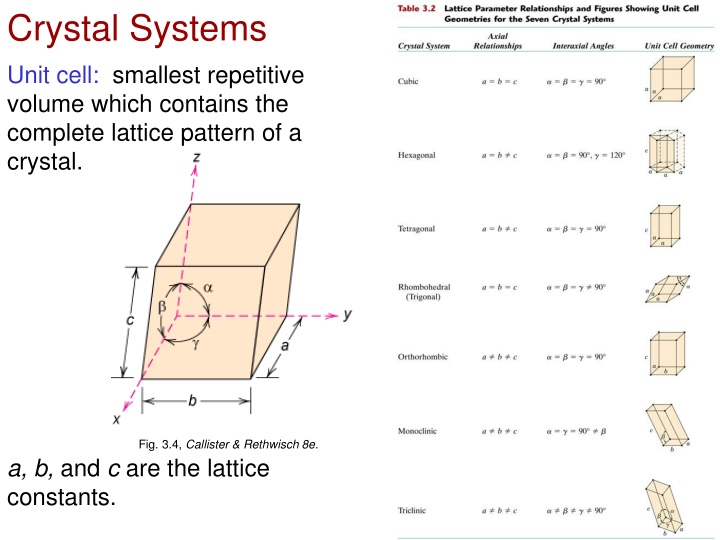
Crystal Systems Unit cell: smallest repetitive volume which contains the complete lattice pattern of a crystal. Fig. 3.4, Callister & Rethwisch 8e. a, b, and c are the lattice constants. Chapter 3 - 1
Crystal Structure and Crystal System Q. What is the difference between crystal structure and crystal system? A: A crystal structure is described by both the geometry of, and atomic arrangements within, the unit cell, whereas a crystal system is described only in terms of the unit cell geometry. For example, face-centered cubic and body-centered cubic are crystal structures that belong to the cubic crystal system. Chapter 3 - 2
Crystal Systems & Bravais Lattices Chapter 3 - 3
Point Coordinates Point coordinates for unit cell center are a/2, b/2, c/2 z 111 c Point coordinates for unit cell corner are 111 y 000 b a x Chapter 3 -
Point coordinates for all atom positions for a BCC unit cell Chapter 3 - 5
Crystallographic Directions Algorithm z 1. Vector repositioned (if necessary) to pass through origin. 2. Read off projections in terms of unit cell dimensions a, b, and c 3. Adjust to smallest integer values 4. Enclose in square brackets, no commas [uvw] y x ex:1, 0, => 2, 0, 1 => [201] -1, 1, 1 where overbar represents a negative index [111] => Chapter 3 - 6
Crystallographic Directions OA AO families of directions <uvw> All cell edges: All face diagonals: All body diagonals: Chapter 3 - 7
Problem 3.32 3.32 Determine the indices for the directions shown in the following cubic unit cell: Chapter 3 - 8