Cubic Tangent Circle
Graphically analyze a cubic function's roots A, B, and C, find point M as the center of a circle passing through B and C, determine the equation of the tangent at M, and check its accuracy by algebraic calculations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
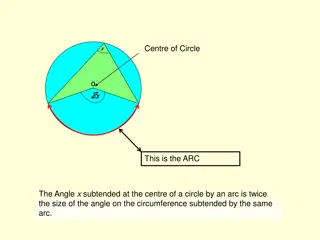
You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0) and (?,0), respectively. Define the function.
Find the coordinates of point M, which lies on the graph ? = ?(?), and is the centre of the circle that passes through B and C.
Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy.
Equation of the cubic: ? = ? ? ? ? ? ? ? = ? ? ?2 ? + ? ? + ?? y = ?3 ? + ? + ? ?2+ ?? + ?? + ?? ? ??? ?? ??= 3 ?2 2 ? + ? + ? ? + ?? + ?? + ?? ?+? 2 ? + ? 2 At M, ??= ?-coordinate of M , 2 ?? ??= 3 ? + ? 2 2 ? + ? + ? + ?? + ?? + ?? ?? ??=3 4 ? + ?2 ?2+ 2?? + ?2 Gradient at M ?? ??= , ? + ?2 At M, ??= 4 ?+? 2 ?+? 2 ? ?+? 2 ? ?+? 2 ? ??= = ?+? 2 ? ? 2 2 2? + ? + ? ?-coordinate of M = 82? ? ? ? ?2
Equation of tangent: 82? ? ? ? ?2= (we are already using c) ? = ?? + ? ??= ???+ ? ?+? 2 ? ?2 + ? 4 ? = ? ? ?2 4 ? = ? ?2 ? + ? ? ?2 4 4 ? = ? ?2 ? ? 4 When ? = 0, ? = ?. Therefore, the tangent passes through the first root, EVERY TIME. How accurate was your tangent?
Note to teacher The same will work if they started with the first two roots, i.e. the tangent should then go through the third. In fact, the tangent at the midpoint of any pair of roots will go through the remaining root! With thanks to Mark Richards of Lancaster Grammar Schools for Girls.
You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. SIC_19
You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. SIC_19 SIC_19 You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. SIC_19 SIC_19
A B C A SIC_19
A B C B SIC_19
A B C C SIC_19
A B C D SIC_19
You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. SIC_19 SIC_19 You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. SIC_19 SIC_19
A B C E SIC_19
A B C F SIC_19
A B C G SIC_19
A B C H SIC_19
You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. SIC_19 SIC_19 You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. You have the graph of a cubic function, ? = ?(?). The roots of the equation ?(?) = 0 are labelled A, B and C. They have coordinates (?,0),(?,0)and(?,0), respectively. Define the function. Find the coordinates of point M, which lies on the graph? = ?(?), and is the centre of the circle that passes through B and C. Draw a tangent to the graph at M and determine where it cuts the ?-axis. Use algebra to work out the equation of the tangent to check your accuracy. SIC_19 SIC_19
A B C I SIC_19
A B C J SIC_19
A B C K SIC_19
A B C L SIC_19