Cylindrical Coordinates in Advanced Mathematics
Explore the concept of cylindrical coordinates, a three-dimensional coordinate system used to specify a point's location based on radial distance, azimuthal angle, and height. Learn about conversions between cylindrical and Cartesian coordinates, along with practical applications in various fields like computer animation and electrical engineering.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Cylinder Coordinates Name of teacher :Dr. Mazin R Khalil Advanced Mathematics2 ME212 Semester 4 Week: 12 Date:21/5/2024
Objectives To teach the students the cylinder coordinates and their characteristics
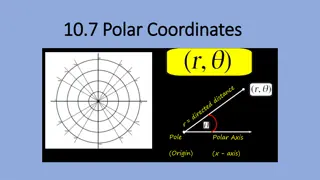
Cylindrical Coordinate System? A three-dimensional coordinate system that is used to specify a point's location by using the radial distance, the azimuthal, and the height of the point from a particular plane is known as a cylindrical coordinate system.
Cylindrical Coordinates Conversions Many three-dimensional coordinate systems exist such as the spherical and the cylindrical coordinate system. With the help of trigonometry, coordinates can be converted from one system to another. Some important conversions are listed below. Cylindrical Coordinates to Cartesian Coordinates Cartesian coordinates can also be referred to as rectangular coordinates. To convert cylindrical coordinates (r, , z) to cartesian coordinates (x, y, z), the steps are as follows:
When polar coordinates are converted to cartesian coordinates the formulas are, x = rcos y = rsin z=z
Cartesian Coordinates to Cylindrical Coordinates The equations that can be used to convert Cartesian coordinates to cylindrical coordinates are as follows: r2= x2+ y2 Tan = y / x z = z Cylindrical Coordinate System Applications Cylindrical coordinate systems are best used when dealing with cylindrical systems such as the volume of a water tank. Other applications of cylindrical coordinates are given below: In computer animation, cylindrical coordinates are used to locate positions on a curved cylindrical surface. When an object is moving on a curved cylindrical trajectory then physicists and engineers use cylindrical coordinates to analyze the motion. Cylindrical coordinates are used to design applications that make use of alternating currents.
Examples on Cylindrical Coordinates Example 1: Express the cylindrical coordinates (4, 2 / 3, -2) as rectangular coordinates. .1 Solution: Using conversion equations, x = rcos = 4 cos (2 / 3) = -2 y = rsin = 4 sin (2 / 3) = 2 3 z = -2 Answer: x = -2, y = 2 3, z = -2
Example 2: Express Cartesian coordinates (1, -3, 5) as cylindrical coordinates. .1 Solution: Using conversion equations, r2= x2+ y2 r2= 12+ (-3)2 r = 10, - 10. As r is a distance we only consider the positive value. tan = y / x = -3 / 1 tan = -3 = -1.24 .2 As the x coordinate is positive and y is negative thus, the value of will lie between 3 / 2 .3 and 2 . = 2 -1.24 .4 = 5.03 radian z = 5 Answer: (1, -3, 5) can be written as ( 10, 5.03, 5) in cylindrical coordinates.
Find the z-limits of integration Find the r-limits of integration Find the theta limits of integration.
References 1. Thomas' Calculus" 11th edition 2. Calculus Early Transcendental Functions" by Ron Larson and Bruce Edwards