Data Encryption and Multiplicative Inverse in Computer Engineering Algebra
Explore concepts in data encryption and computer engineering algebra, covering topics like the Extended Euclidean Theorem, finding GCD using factorization, linear combination of numbers, and calculating multiplicative inverses. Dr. Fatimah Al-Ubaidy guides students through examples and explanations for practical application. Discover how to utilize the Extended Euclidean algorithm to unlock encryption secrets and solve mathematical challenges in computer engineering.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
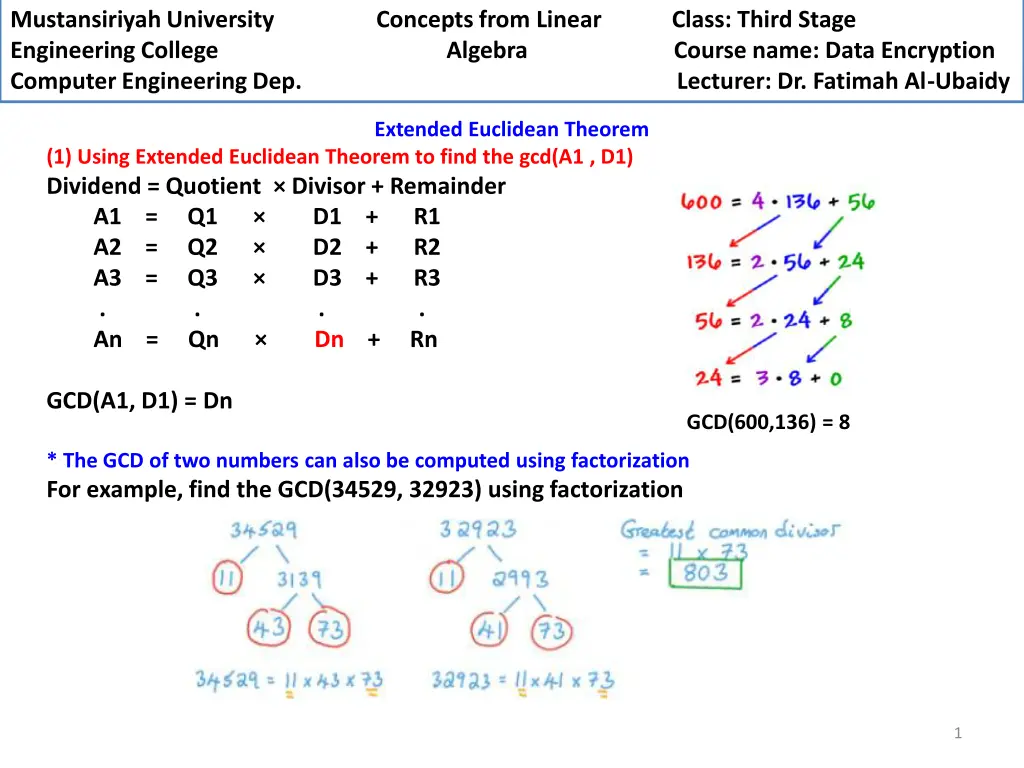
Mustansiriyah University Engineering College Algebra Course name: Data Encryption Computer Engineering Dep. Lecturer: Dr. Fatimah Al-Ubaidy Concepts from Linear Class: Third Stage Extended Euclidean Theorem (1) Using Extended Euclidean Theorem to find the gcd(A1 , D1) Dividend = Quotient Divisor + Remainder A1 = Q1 D1 + R1 A2 = Q2 D2 + R2 A3 = Q3 D3 + R3 . . . . An = Qn Dn + Rn GCD(A1, D1) = Dn GCD(600,136) = 8 * The GCD of two numbers can also be computed using factorization For example, find the GCD(34529, 32923) using factorization 1
Mustansiriyah University Engineering College Algebra Course name: Data Encryption Computer Engineering Dep. Lecturer: Dr. Fatimah Al-Ubaidy Concepts from Linear Class: Third Stage (2) Use Extended Euclidean algorithm to find the linear combination of two numbers Extended Euclidean algorithm also finds integer coefficients x and y such that: ax + by = gcd(a, b) This is can be done by reversing the steps in the Euclidean algorithm. 2
Mustansiriyah University Engineering College Algebra Course name: Data Encryption Computer Engineering Dep. Lecturer: Dr. Fatimah Al-Ubaidy Concepts from Linear Class: Third Stage (3) Use Extended Euclidean Theorem to find the multiplicative inverse Example (1): Find multiplicative inverse of 211 mod 101? Step1: 211 = 2 101 + 9 101 = 11 9 + 2 9 = 4 2 + 1 Step2: Then, work backwards: 1 = 9 4 2 = 9 4 (101 11 9) = (9) 4 (101) + 44 (9) = 45 (9) - 4 (101) = 45 (211 2 101) 4 (101) = 45 (211) 90 (101) 4 (101) = 45 (211) 94 (101) 1 = 45 211 94 101 Step3: Finally, take mod 101: 1 mod 101 = 45 211 mod101 94 101 mod 101 1 45 211 mod 101 211-1 mod 101 = 45 To verify the solution, we multiply the number by its inverse 211 45 = 1 mod 101 ---- > 45 = ( 1 + 101 k ) / 211 at k = 94 3
Mustansiriyah University Engineering College Algebra Course name: Data Encryption Computer Engineering Dep. Lecturer: Dr. Fatimah Al-Ubaidy Concepts from Linear Class: Third Stage Example (2): Find multiplicative inverse of 43 mod 660? Step1: 660 = 15 43 + 15 43 = 2 15 + 13 15 = 1 13 + 2 13 = 6 2 + 1 Step2: Then, work backwards: 1 = 13 6 2 = 13 6 (15 1 13) = 7 (13) - 6 (15) = 7 (43 2 15) 6 15 = 7 (43) 20 (15) = 7 (43) 20 (660 15 43) = 307 (43) 20 (660) Step3: Finally, take mod 600: 1 mod 660 = 307 43 mod 660 20 660 mod 660 1 43 307 mod 660 43-1 mod 660 = 307 To verify the solution, we multiply the number by its inverse 43 307 = 1 mod 660 4






















