DC Circuits and Kirchhoff's Rules for Resistors

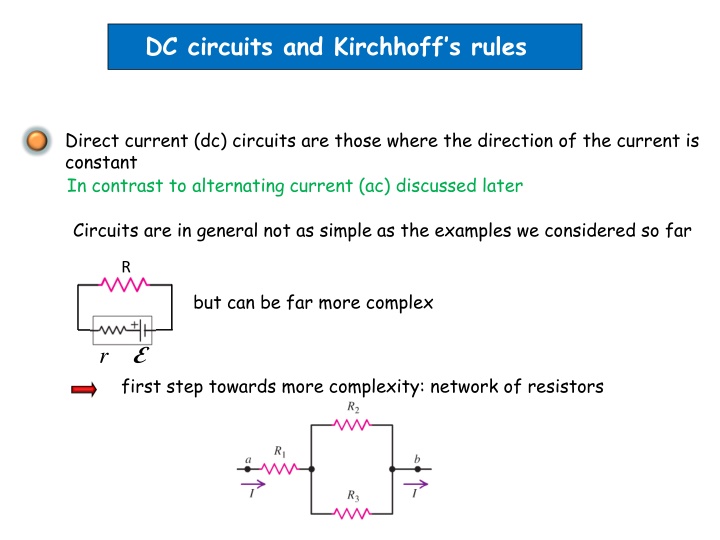
DC circuits and Kirchhoffs rules Direct current (dc) circuits are those where the direction of the current is constant In contrast to alternating current (ac) discussed later Circuits are in general not as simple as the examples we considered so far R but can be far more complex E first step towards more complexity: network of resistors r

Resistors in series and parallel For any combination of resistors we can always find a single resistor replacing the combination resulting in the same I and V Vab Req Vab How to find this equivalent resistance systematically Let s start with resistors in series = + + We know: V V V V and I is the same for R1,2,3 ab ax xy yb

= + + = = = With , , V V V V V R I V R I V R I and 1 2 3 ax xy yb ab ax xy yb ( ) = + + = + + = R I R I R I R R R I V R I 1 2 3 1 2 3 ab eq = + + Rq here R R R e 1 2 3 This can be generalized to any number of resistors using Req(n+1)=Req(n)+R(n+1) and Req(1)=R1 into = + + + R ... R R R for resistors in series e 1 2 3 q

Resistors in parallel = V R I ab eq The major step towards a rule for the equivalent resistance for the parallel circuit is to realize: i) Voltages across all R1,2,3 are identical = = = V R I R I R I 1 1 2 2 3 3 ab ii) Current I splits into currents I1,2,3 such that I=I1+I2+I3 1 1 R 1 R 1 R I I I I = = + + = + + 1 2 3 V R V V V ab eq 1 2 3 ab ab ab This again can be generalized to any number of resistors 1 1 R 1 R 1 R = + + + ... for resistors in parallel R 1 2 3 eq

Clicker question To switch off the electric candles decorating the Xmas tree of my friends in good old Germany, they can remove just one candle out of its socket. This lazy trick works because 1) The electric candles are connected in parallel 2) The electric candles are connected in series 3) There is no relation to what we just learned. Light bulbs are no resistors. The trick works because of Santa.