Decompositions into Squares: Decidability in Complexity Theory
Explore the concept of decomposing strings into squares in complexity theory, focusing on decidability and undecidability. Can a string composed of 0s and 1s be decomposed into squares? Delve into the implications of this problem and the challenges in determining its decidability, shedding light on the complexities of computation. Instructor: William Hoza.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
CMSC 28100 Introduction to Complexity Theory Complexity Theory Spring 2024 Instructor: William Hoza 1
Midterm exam Midterm exam will be in class on Wednesday, April 17 To prepare for the midterm, you only need to study the material up to this point The midterm will be about decidability and undecidability 2
Which problems Which problems can be solved can be solved through computation? through computation? 3
Decompositions into squares Let SQUARES = ?? ? 0,1 We say that a string ? {0,1} can be decomposed into squares if there exist ?1,?2, ,?? SQUARES such that ? = ?1?2 ?? Example: 00100111 = 001 001 1 1 Example: 1001 cannot be decomposed into squares 4
Decompositions into squares ? 0,1 ? can be Let DECOMPOSABLE-INTO-SQUARES = { } decomposed into squares Is DECOMPOSABLE-INTO-SQUARES decidable? A: Yes B: No D:It s not a language, so the question doesn t make sense C: It depends on the encoding Respond at PollEv.com/whoza or text whoza to 22333 5
Decompositions into squares ? 0,1 ? can be Let DECOMPOSABLE-INTO-SQUARES = { } decomposed into squares Claim:DECOMPOSABLE-INTO-SQUARES is decidable Proof sketch: Given ? 0,1 , try all possible decompositions of ? into substrings: ? = ?1?2 ?? Check whether ?? SQUARES for each ? If we find a decomposition into squares, accept; otherwise, reject. 6
Decompositions into squares DECOMPOSABLE-INTO-SQUARES is decidable So Can we actually decide it? 7
Our algorithm is so slow that its worthless Can the following string be decomposed into squares? 001100110010100110000000101001100000011111111011111111010110101110100 100100111010010010011010101011111110001011111110001010011010100110101 Checking all possible decompositions would take longer than a lifetime One begins to feel that DECOMPOSABLE-INTO-SQUARES might as well be undecidable 8
Which problems Which problems can be solved can be solved through computation? through computation? 9
Refining our model The mathematical model we have studied so far: Decidable vs. undecidable Now we will refine our model to take into account the fact that in real life, we only have a limited amount of time (and other resources) Complexity theory 10
Analogy: Gravity In an introductory physics class, we might model gravity as a constant downward force of 9.8 N/kg In a more advanced physics class, we might use a more sophisticated model of gravity: ? = ? ?1 ?2 ?2 11
Theory vs. practice Disclaimer: Our theoretical model will still not be perfectly accurate! Sometimes, we might categorize a problem as tractable even though it is not actually solvable in practice Other times, we might categorize a problem as intractable even though it is actually solvable in practice 12
Theory vs. practice Physics analogy: Newton s universal law of gravitation (? = ? ?1 ?2 ?2) is a fantastic approximation in many cases, but it does not correctly predict Mercury s motion around the sun! all models are wrong, but some are useful. George Box Even though our model of tractability will not be completely accurate, it will still give us real insights into the nature of computation 13
Time complexity Let ? be a Turing machine with input alphabet The time complexity of ? is a function ??: defined as follows: ??? = max ? ?running time of ? on ? We are focusing on the worst-case ?-symbol input 14
Deciding a language in time ? Let ? be a language and let ?: be a function Definition: We say that ? can be decided in time ? if there exists a Turing machine ? such that ? decides ?, and If we let ??: be the time complexity of ?, then for every ?, we have ??? ? ? 15
Scaling behavior We will mainly focus on the limiting behavior of ? ? as ? How quickly does the time complexity ? ? increase when we increase the input length ?? 16
Asymptotic analysis Asymptotic analysis 17
Asymptotic analysis Two possible time complexities: ?1? = 3?2+ 14 ?2? = 2?2+ 64? + ? When ? is large, the leading ? ?2 term dominates We will ignore the low-order terms and the leading coefficient ? We focus on the ?2part ( quadratic time ) 18
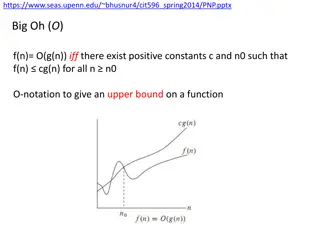
Big-? notation 3?2+ 14 and 2?2+ 64? + ? are both ? ?2 More generally, let ?,?: be any two functions We say that ? is ? ? if there exist ?,? such that for every ? > ? , we have ? ? ? ? ? Notation: ? ? ? or ? ? ? or ? = ? ? 19
Big-? notation examples 3?2+ 14 is ? ?2 3?2+ 14 is ? ?2+ ? 3?2+ 14 is ? ?3 3?2+ 14 is not ? ?1.9 20
Big- and big- Let ?,?: be any two functions We say that ? is ? if there exist ? 0,1 and ? such that for every ? > ? , we have ? ? ? ? ? We say that ? is ? if ? is ? ? and ? is ? 21
Big- and big- examples 0.1?2+ 14 is ?2 and ? , but not ?3 0.1?2+ 14 is ?2 and ?2+ 2?1.4, but not ? Let ? ? = 23?+4. Which of the following statements is false? A:? ? is 2? B:? ? is 2 ? D:? ? is ? 2? C:?(?) is 23? Respond at PollEv.com/whoza or text whoza to 22333 22