Deformation Techniques in Computer Graphics
Discover the Complex Barycentric Coordinates method for visually pleasing planar shape deformations in computer graphics. Learn about bounded distortion mappings and harmonic mappings for efficient shape manipulation. Implement techniques using C++ and Matlab with Autodesk Maya for visualizations and user interface creation. Explore the tradeoff between global changes and local detail preservation in shape deformation.
Uploaded on | 1 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
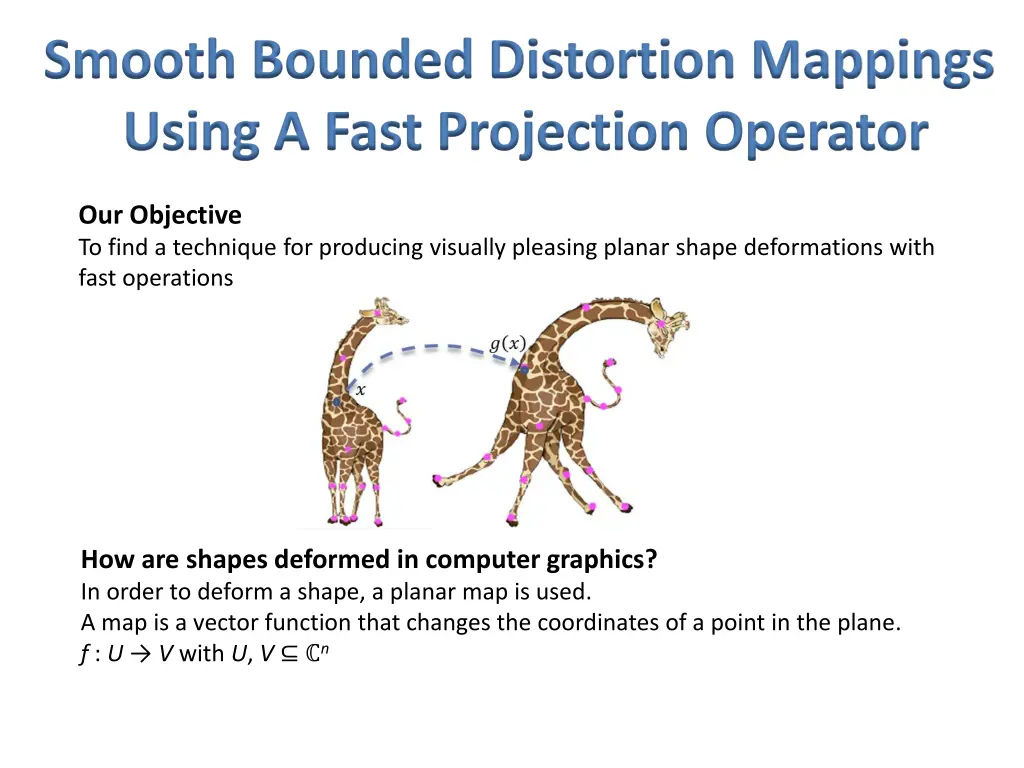
Smooth Bounded Distortion Mappings Using A Fast Projection Operator Our Objective To find a technique for producing visually pleasing planar shape deformations with fast operations How are shapes deformed in computer graphics? In order to deform a shape, a planar map is used. A map is a vector function that changes the coordinates of a point in the plane. f : U V with U, V n
the project We shall study and implement Dr. Weber s technique for computing bounded distortion harmonic mappings We want to turn this Into this And not get this The project will be implemented in c++ and Matlab Autodesk Maya will be used for graphic visualizations and for creating the user interface Matlab will be used for linear algebra computations CVX will be used for solving convex optimization problems
Complex Barycentric Coordinates with Applications to Planar Shape Deformation Ofir Weber, Mirela Ben-Chen and Craig Gotsman The problem of shape deformation There is a tradeoff between global changes and local detail preservation VS Challenges: Shape preservation we would like the overall shape to have bounded distortion Exact Boundary Behavior we would like the shape to stay within the control cage Efficiency fast computation time Easy to control
The Solution We shall use complex barycentric coordinates Pros: The resulting function g is holomorphic, and infinitely differentiable Reproduces similarity transformations Small extra cost in computational complexity, in pre-process time only Work well with P2P - An intuitive user interface for the modeler Cons: Exact Boundary Behavior target image may deviate from the cage Mapping is not injective Scale distortion is unbounded