Discrete Mathematics for Computer Science - GCD and Euclid's Algorithm Explained
Dive into the world of Discrete Mathematics with Professor Shachar Lovett as you explore the concepts of Greatest Common Divisor (GCD) and Euclid's Algorithm. Learn how to compute GCD, understand prime factorization, and discover the fast computation of GCD using Euclid's Algorithm.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
CSE 20: Discrete Mathematics for Computer Science Prof. Shachar Lovett
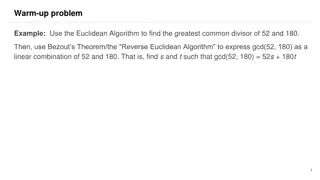
2 Today s Topics: 1. GCD 2. Euclid s algorithm 3. Extended Euclid s algorithm
3 1. GCD The poor man version of prime factorization
4 GCD Greatest common divisor Given two positive integers a,b, their GCD is the largest integer n such that n|a and n|b
5 GCD What is GCD(20,30)? A. 5 B. 10 C. 20 D. 30 E. Other
6 GCD What is GCD(101281371,347832984723)?
7 GCD How can we compute GCD(a,b)? Simple way: (i) Compute prime factorization of a,b (ii) Take common primes and prime powers Example: if a=2103859 and b=21735 then GCD(a,b)=21035 However, we believe that computing the prime factorization of large numbers is hard Euclid s algorithm provides a much faster way
8 2. Euclid s algorithm Fast GCD
Euclids algorithm Euclid(a,b): Input: ?,? ? Output: ? = gcd(?,?) While b>0: a. x=a mod b b. a=b c. b=x Return a 1. 2.
Euclids algorithm Euclid(a,b): Input: ?,? ? Output: ? = gcd(?,?) (a,b) While b>0: a. x=a mod b b. a=b c. b=x Return a 1. (b,a mod b) 2.
Euclids algorithm Euclid(a,b): Input: ?,? ? Output: ? = gcd(?,?) 1. While b>0: ?,? (?,? ??? ?) 2. Return a
Euclids algorithm Example run: a=20, b=30 Euclid(a,b): Input: ?,? ? Output: ? = gcd(?,?) a 20 30 20 10 b 30 20 10 0 1. While b>0: ?,? (?,? ??? ?) 2. Return a
Euclids algorithm The same basic questions 1. Does it always terminate? 2. Does it return the correct answer? 3. How fast is it?
Euclids algorithm: termination Euclid(a,b): Input: ?,? ? Output: ? = gcd(?,?) Loop invariant (after 1st iteration): ? > ? 1. While ? > 0: ?,? (?,? ??? ?) 2. Return a
Euclids algorithm: termination Euclid(a,b): Input: ?,? ? Output: ? = gcd(?,?) Loop invariant (after 1st iteration): ? > ? 1. While ? > 0: ?,? (?,? ??? ?) 2. Return a Loop beginning: (a,b) Loop end: (b, a mod b) By definition, ? ??? ? 0, ,? 1 and hence (a mod b) < b
Euclids algorithm: termination Euclid(a,b): Input: ?,? ? Output: ? = gcd(?,?) Loop invariant (after 1st iteration): ? > ? 1. While ? > 0: ?,? (?,? ??? ?) 2. Return a The value of a keeps decreasing, which proves termination
Euclids algorithm: correctness Euclid(a,b): Input: ?,? ? Output: ? = gcd(?,?) g=gcd(a,b) 1. While ? > 0: ?,? (?,? ??? ?) 2. Return a
Euclids algorithm: correctness Need to prove the following lemma Lemma: ?,? 1,gcd ?,? = gcd(?,? ??? ?)
Euclids algorithm: correctness Need to prove the following lemma Lemma: ?,? 1,gcd ?,? = gcd(?,? ??? ?) Proof: we will actually show ? 1, ? ? ? ? (? ? ? ? ??? ? ) In particular, the largest such m is (by definition) the GCD, and so gcd ?,? = gcd(?,? ??? ?)
Euclids algorithm: correctness Lemma: ?,? 1,gcd ?,? = gcd ?,? ??? ? Proof ( ): ? ? ? ? (? ? ? ? ??? ? ) Let ? = ?? + ?, where ? = ? ??? ?, ? = ? ??? ?. If ?|?,?|? then ? = ??, ? = ??, where ?,? ?. Then: ? ??? ? = ? = ? ?? = ?? ?? ? = ? ? ?? So, ?|(? ??? ?).
Euclids algorithm: correctness Lemma: ?,? 1,gcd ?,? = gcd ?,? ??? ? Proof ( ): ? ? ? ? (? ? ? ? ??? ? ) Let ? = ?? + ?, where ? = ? ??? ?, ? = ? ??? ?. If ?|?,?|? then b = ??, q = ??, where ?,? ?. Then: ? = ?? + ? = ?? ? + ?? = ?(?? + ?) So, ?|?.
Euclids algorithm: correctness Euclid(a,b): Input: ?,? ? Output: ? = gcd(?,?) g=gcd(a,b) Proved! 1. While ? > 0: ?,? (?,? ??? ?) 2. Return a
Euclids algorithm: speed Euclid(a,b): Input: ?,? ? Output: ? = gcd(?,?) How many iterations? 1. While ? > 0: ?,? (?,? ??? ?) 2. Return a
Euclids algorithm: speed Consider one iteration: ?,? (?,? ??? ?) We know that a,b become smaller But by how much?
Euclids algorithm: speed Consider one iteration: ?,? (?,? ??? ?) We know that a,b become smaller But by how much? Intuition: Since ? ??? ? {0,..,? 1}, on average ? ??? ? ?/2. Hence, value of b decreases by a factor of 2 at each iteration (so log(b) iterations will be needed) Can we justify this?
Euclids algorithm: speed Consider one iteration: ?,? (?,? ??? ?) Lemma: ? + ? 3 2(? + ? ??? ? ) Sum decreases by 3/2 at each iteration; So, we need at most ~log(a+b) iterations In fact, at most ~log(b) iterations, since after the first iteration, both values are at most b
Euclids algorithm: speed Consider one iteration: ?,? (?,? ??? ?) Lemma: ? + ? 3 2(? + ? ??? ? ) Proof: Since ? > ? > ? ??? ?, and since b|? (? ??? ?), we must have ? ? ??? ? ?. So: ? ? + (? ??? ?) ? =? (i) 2+? 2 1 2? + ? ??? ? (ii) ? + ? 3 2(? + ? ??? ? )
28 3. Extended Euclid s algorithm Using algorithms to do math!
Extended Euclids algorithm Theorem: ?,? ? ?,? ? ?? + ?? = gcd(?,?) (this is called Extended Euclid s algorithm) Example: a=3, b=5, gcd(a,b)=1 3*(-3)+5*2 = 1 (solution: x=-3, y=2)
Extended Euclids algorithm Theorem: ?,? ? ?,? ? ?? + ?? = gcd(?,?) (this is called Extended Euclid s algorithm) Example: a=3, b=5, gcd(a,b)=1 3*(-3)+5*2 = 1 (solution: x=-3, y=2) The proof will use our analysis of Euclid s algorithm So, even though the theorem has nothing to do with algorithms, the proof will use an algorithm!
Extended Euclids algorithm Theorem: ? ? 1 ?,? ? ?? + ?? = gcd(?,?) Proof (by strong induction on b): Base case: b=1, so gcd(a,1)=a, can take x=1,y=1 Inductive case: We use the identity: gcd ?,? = gcd(?,? ??? ?). Since ? > ? ??? ?, by the inductive assumption ? ,? ?,?? + ? ??? ? ? = gcd b,a mod b = gcd ?,? Let ? = ?? + ?, where ? = ? ??? ?, ? = ? ??? ?. Then: ?? + ? ?? ? = gcd ?,? Take ? = ? ,? = ? ?? so that ?? + ?? = gcd ?,? .