Dynamics of Romeo and Juliet's Affections
Explore the oscillatory dynamics of Romeo and Juliet's love and hate relationships through state space diagrams, nullcline angles, and trajectory loops. Witness how their affections form closed cycles, sinusoidal movements, and stability patterns with crossed nullclines.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
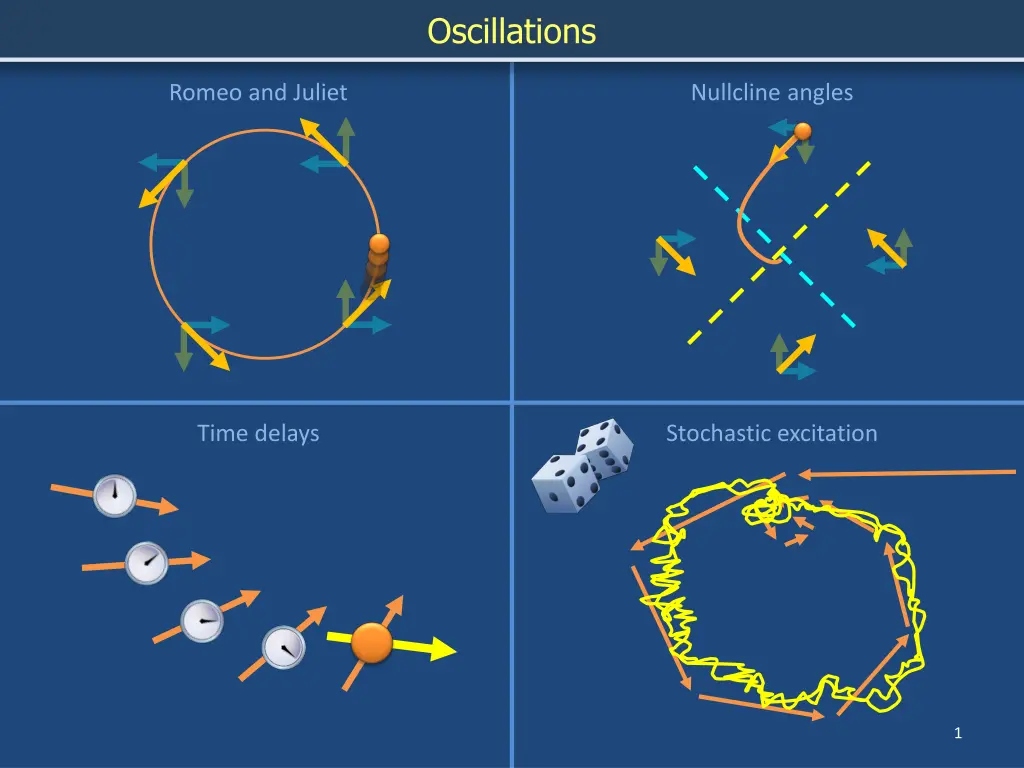
Oscillations Romeo and Juliet Nullcline angles Time delays Stochastic excitation 1
Romeo and Juliets affections form a state space J = Love that Juliet professes for Romeo R = Love that Romeo professes for Juliet J Juliet professes love, but Romeo professes hate Both profess love R Romeo professes love, but Juliet professes hate Both profess hate 2
Juliets dynamics Juliet professes more and more love when Romeo expresses love J ?? ??= ? R 3
Romeos dynamics Romeo professes less and less love when Juliet professes love J ?? ??= ? ?? ??= ? R 4
Trajectory of Romeo and Juliets dynamics form a closed loop Romeo and Juliet chase each other around in a perpetual soap opera J ?? ??= ? ?? ??= ? R 5
Romeo and Juliets dynamics are sinusoidal J ?? ??= ? ?? ??= ? R ?2? ??2= ?? ?? ?2? ??2= ? ? = ?0cos ? ? = ?0sin ? 6
Oscillations Romeo and Juliet Nullcline angles Time delays Stochastic excitation 7
Derivatives can change sign at nullclines J ?? ??= 0 R 8
Derivatives can change sign at nullclines J ?? ??= 0 R 9
Oscillations Romeo and Juliet Nullcline angles Time delays Stochastic excitation 14
Time delay J R 15
Time delay J Current state Previous state R 16
Oscillations Romeo and Juliet Nullcline angles Time delays Stochastic excitation 17
Stochastic excitation J R 18
Stochastic excitation J R 19
Stochastic excitation J R 20