Efficient Data Structures for External Memory Top-k Queries
Explore efficient data structures and algorithms for handling top-k queries in external memory settings with sublogarithmic updates. Topics include external memory models, priority search trees, and 3-sided range reporting. Discover novel approaches and results from various research studies.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
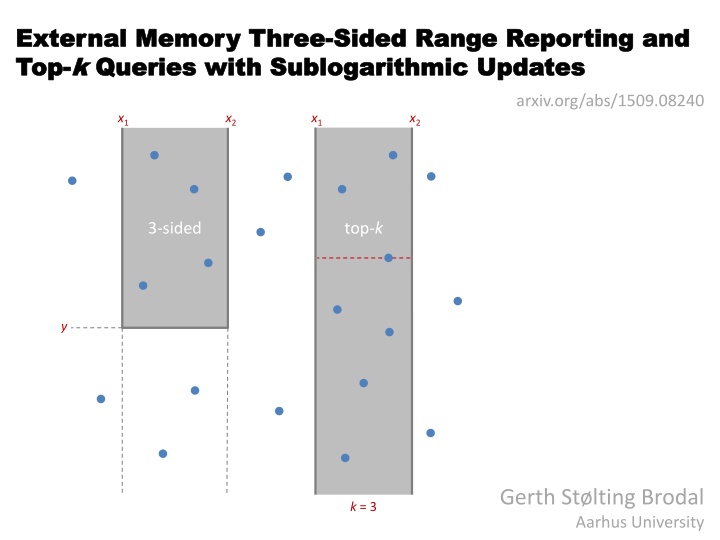
External Memory Three External Memory Three- -Sided Range Reporting and Sided Range Reporting and Top Top- -k k Queries with Queries with Sublogarithmic Sublogarithmic Updates Updates arxiv.org/abs/1509.08240 x1 x2 x1 x2 3-sided top-k y Gerth St lting Brodal Aarhus University k = 3
Internal Memory Priority Search Trees McCreight 1985 Frederickson 1993 Properties leaves x-sorted point p stored on leaf p-to-root path y-values satisfy heap-order L C Q M D G J N Updates O(log n) 3-sided & top-k O(k + log n) A E H I K P B B C D E F F G H I J K L M N O O P A Q A L Q + 3-sided C + D M G + L J + D G N E y + M P H A I + heap-ordered N E H B O K M - F J x1 x2 E - G - - F F H I K select k+s largest in O(k+s) time - - - - I J K L
External Memory Model Aggarwal & Vitter 1988 External CPU Internal IO of B consecutive cells M B-tree Bayer & McCreight 1972 Insert, Delete, Search O(log (n/B)) IOs degree B -1 search keys height O(log (n/B)) leaves (B) elements Buffered B-tree Arge 1995 buffer of B delayed updates Search O(log (n/B)) IOs Updates amortized O( /B log (n/B)) IOs
Results Updates Query Ramaswamy , Subramanian 1995 OA(log n log B) O(logBn + k/B) 3-sided Subramanian, Ramaswamy 1995 OA(logBn + (logBn)2/B) O(logBn + k/B + log**B) Arge et al. 1999 O(logBn) O(logBn + k/B) OA (1/ logBn + k/B) O(logBn + k/B) O(logBn + k/B) O(logBn + k/B) OA(1/ logBn + k/B) OA(1/( B1- ) logBn) (static) NEW Afshani et al. 2011 top-k OA((logBn)2) OA(logBn) OA(1/( B1- ) logBn) Sheng, Tao 2012 Tao 2014 k = 3 NEW OA = amortized NEW result : Combination of Arge 1995, Arge et al. 1999, Frederickson 1993, Blum et al. 1973
3-sided Data Structure 3-sided buffers of O(B) delayed insertions and deletions below v external memory priority search tree root stores topmost (B) points efficient structure for accessing children sP sets v degree = B Pv Iv Dv Cv y-sorted x-sorted x1 x2 Insertions / deletions : Update root Pv or add to delayed update buffer Iv / Dv Update buffer overflow : Flush recursively to child with most updates ( B1- ) Leaf overflow : split leaf, and recursively split ancestors of degree +1 Underflowing point buffer Pv : pull elements recursively from children using Cv 3-sided query : i) Identify nodes to visit using Cv structures. ii) flush updates down from ancestors of visited nodes. iii) report from nodes using Pv, Cv and update buffers
Child Structure Cv Arge et al. 1999 3-sided v degree = B Pv Iv Dv Cv Insert / delete s points : O(1 + s/B1- ) IOs 3-sided query : O(1 + k/B) IOs y-samples for range [x1,x2] : O(1) IOs (new) b1,8 b1,5 Capacity : B1+ Insetion /deletion buffer O(B) points O(B ) blocks Catalog block y-samples block (new) b3,5 b6,8 b3,4 y b6,7 b1,2 b1 b2 b3 b4 b5 b6 b7 b8
Top-k Overall Approach find magic y 3-sided query select k-largest x1 x2 x1 x2 top-k 3-sided Superset Answer O(B log (n/B) + k) y k = 3 Blum et al. 1973 All steps require O(log (n/B) + k/B) IOs The 3-sided query is amortized Construct (on demand) a binary heap over every (B) th element in the Cv structures and select the (log (n/B) + k/B) th element using Frederickson 1993
The End Summary Updates Query Ramaswamy , Subramanian 1995 OA(log n log B) O(logBn + k/B) 3-sided Subramanian, Ramaswamy 1995 OA(logBn + (logBn)2/B) O(logBn + k/B + log**B) Arge et al. 1999 O(logBn) O(logBn + k/B) OA (1/ logBn + k/B) O(logBn + k/B) O(logBn + k/B) O(logBn + k/B) OA(1/ logBn + k/B) OA(1/( B1- ) logBn) (static) NEW Afshani et al. 2011 top-k OA((logBn)2) OA(logBn) OA(1/( B1- ) logBn) Sheng, Tao 2012 Tao 2014 k = 3 NEW OA = amortized Open problem : Remove amortization ?
