Efficient Iterative Graph Algorithm Optimization Techniques
Explore techniques such as Block Coordinate Descent that aim to reduce the runtime of iterative graph algorithms by optimizing the number of iterations and runtime per iteration. Learn how these methods can lead to fewer iterations with higher runtime efficiency, enhancing graph analytics scalability.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
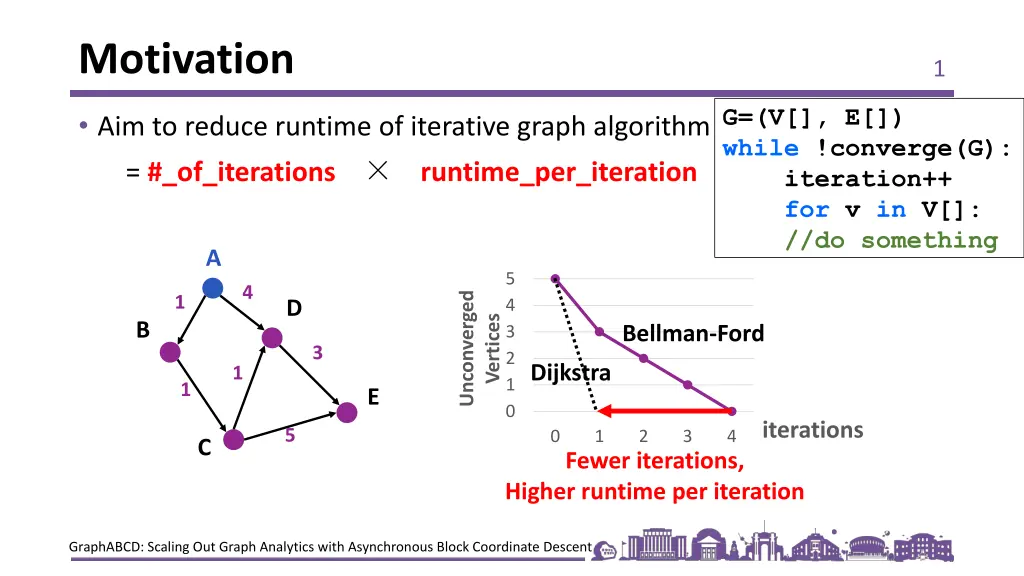
Motivation 1 G=(V[], E[]) while !converge(G): iteration++ for v in V[]: //do something Aim to reduce runtime of iterative graph algorithm = #_of_iterations runtime_per_iteration A 5 4 Unconverged 1 4 D Vertices B Bellman-Ford 3 3 2 Dijkstra 1 1 1 E 0 iterations 5 0 1 2 3 4 C Fewer iterations, Higher runtime per iteration GraphABCD: Scaling Out Graph Analytics with Asynchronous Block Coordinate Descent
Solution: BCD execution model 2 G=(V[], E[]) while !converge(G): iteration++ for v in V[]: //do something Aim to reduce runtime of iterative graph algorithm = #_of_iterations Solution: introduce Block Coordinate Descent (BCD) execution model, an execution model for optimization algorithm, to graph analytics runtime_per_iteration Configuring BCD design parameters reduces #_of_iterations BCD enables efficient asynchronous processing by minimizing synchronization overhead to reduce runtime_per_iteration GraphABCD: Scaling Out Graph Analytics with Asynchronous Block Coordinate Descent
Block Coordinate Descent execution model 3 Until Convergence Partition Graph Choose Block Update Block //SSSP Example G=(V[], E[]) while !converge(G): b=choose_block(G) for v in b: tmp_depth=MAX for ngh in v.ngh: tmp_depth=min(tmp_depth, ngh.depth+distance(v,ngh)) v.depth=tmp_depth GraphABCD: Scaling Out Graph Analytics with Asynchronous Block Coordinate Descent
GraphABCD framework and evaluation 4 CPU Prototyped on Intel HARPv2 CPU+FPGA system Until Convergence Partition Graph Choose Block Scatter Geo-mean speedup of 2.0x on execution time and 4.8x reduction on number of iterations over GraphMat Gather Apply Control Intensive Random Access PE Accelerator Compute Intensive Sequential Access GraphABCD: Scaling Out Graph Analytics with Asynchronous Block Coordinate Descent