Electric Fields and Flux Through Surfaces - Understanding Concepts
Explore electric flux through closed surfaces due to uniform electric fields and the signs of electric flux with point charges outside closed cylindrical surfaces. Learn about divergence of vector fields in specific regions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
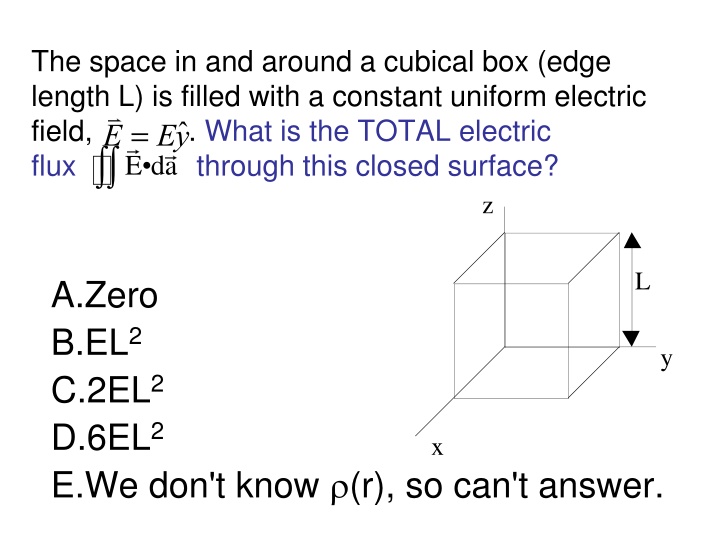
The space in and around a cubical box (edge length L) is filled with a constant uniform electric field, . What is the TOTAL electric flux through this closed surface? E = E y E da z L A.Zero B.EL2 C.2EL2 D.6EL2 E.We don't know (r), so can't answer. y x
A positive point charge +q is placed outside a closed cylindrical surface as shown. The closed surface consists of the flat end caps (labeled A and B) and the curved side surface (C). What is the sign of the electric flux through surface C? (A) positive (D) not enough information given to decide (B) negative (C) zero A q C q B (Side View)
A positive point charge +q is placed outside a closed cylindrical surface as shown. The closed surface consists of the flat end caps (labeled A and B) and the curved side surface (C). What is the sign of the electric flux through surface C? (A) positive (B) negative (C) zero (D) not enough information given to decide q A C q (Side View) B
1.4 Which of the following two fields has zero divergence? I II A) Both do B) Only I is zero C) Only II is zero D) Neither is zero E) ??
1.5 What is the divergence of this vector field in the boxed region? A) Zero B) Not zero C) ???
