Equivalence Relations and Partitions
Equivalence relations are essential in mathematics for understanding relationships between various elements within a set. This content explores reflexive, symmetric, and transitive relations, along with examples demonstrating the concept's application. Discover the significance of partitions in defining equivalence classes and establishing relationships based on certain properties.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
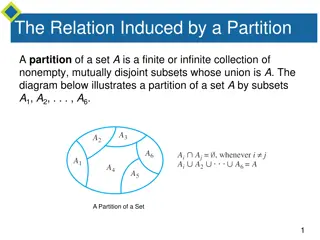
Equivalence Relation & Partitions Equivalence Relations & Partitions
Definition(Different Types of Relations): Let A be a non-empty set and be a relation on A . Then is said to be a a)Reflexive Relation if (a,a) i.e.,a a,for each a A ; b)Symmetric Relation if (a,b) implies that (b,a) i.e., for any two elements a,b A,whenever a b holds then b a holds; c)Transitive Relation if for any three elements a,b,c A,whenever a b and b c hold then a c holds
Equivalance Relation The relation is said to be equivalance if it is reflexive,symmetric transitive.
Examples: Question 1:Let us assume that is a relation on the set Z of integers defined by x y if and only if x-y is an integer. Prove that is an equivalence relation on Z. Solution:Reflexive: Consider x Z,then x x = 0 which is an integer. Therefore x x. Symmetric: Consider x , y Z and x y.Then x y is an integer. Thus, y x = ( x y), y x is also an integer. Therefore y x. Transitive: Consider x , y Z , x y and y z. Therefore x-y and y-z are integers. According to the transitive property, ( x y ) + ( y z ) = x z is also an integer. So that x z. Thus, is an equivalence relation on Z.