Estimating Branching Fractions in B Meson Decays: A Study in Flavor Physics

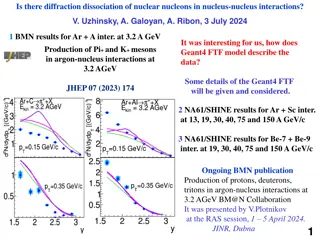
University of Urmia Department of Physics Urmia, Iran Estimating the branching fraction for ?? ?(??)??decay Behnam Mohammadi Diffraction 2016 Santa Tecla di Acireale, Italy September 2-8, 2016 31 05 25 1

Outlines: Introduction Factorization Amplitude of the ?? ?(??)??decay Branching fraction Numerical results Conclusion 31 05 25 2

Introduction: B meson decays to two-body final states containing a charmonium resonance such as a ?(2?) offer a powerful way of studying electroweak transitions. Such decays probe charmonium properties and play a role in the study of CP violation and mixing in the neutral B system. The study of CP violation is one of the most important topics in flavor physics. In ?0decays, the phenomenon of CP violation has been extensively studied at BaBar, Belle and LHCb, which confirmed many predictions of the Standard Model (SM) Recently the Belle collaboration have reported the first measurement of the ?0 ? 2? ?0branching fraction based on the full ? 4? data set of 722 106? ? pairs collected by the Belle detector at the KEKB asymmetric- energy ?+? collider [1]. [1] Belle Collaboration, V. Chobanova, et al, Phys. Rev. D 93 (2016) 031101. 31 05 25 3

Introduction: The estimates of the branching fractions in the non-leptonic charmonium two-body decay rates for the ?0 ? 2? ?0decay and the same decays of ?+ ? 2? ?+, ?0 ? 2? ?0, and ?+ ? 2? ?+are considered. These estimates are based on a generalized factorization approach making use of leading order (LO) and next-to-leading order (NLO) contributions. The results show that when the large enhancements from the known NLO contributions by using the QCD factorization approach are taken into account, all estimates become in good agreement with the experimental results [1]. The CP violating asymmetry for ?0 ? 2? ?0decay, unlike similar decays of ?+ ? 2? ?+, ?0 ? 2? ?0, and ?+ ? 2? ?+, is not available, but the last three decays allow access to the CP violating angle 1= ( ?????? These decay modes have similar calculation with ?0 ? 2? ?0decay, so CP violation estimating of them can be generalized to it in a future work. )/(?????? ) at first order (tree) and higher order (penguin). 31 05 25 4

Factorization The approach which has often been employed in non-leptonic heavy hadron decays is based on factorization. The matrix elements < ?1?2|????|? > in the factorization approach can be expressed as a product of two factors, one form factor < ?1|?1|? > and the other decay constant < ?2|?2|0 >. The resulting matrix elements of the current operators ?? have been mostly calculated in well-defined theoretical frameworks, such as Lattice-QCD, QCD sum rules and potential models. In the decays of ? ?1?2, the energy of the ?1and ?2mesons should be large and their masses should be small and hence factorization give a good approximation. In the case of, the final state involves both the charm and light mesons, also have genuine short distance contributions which can be calculated using perturbation theory. 31 05 25 5

Factorization And also in the case of pure annihilation and pure penguin (b s and b d transitions) decays can be calculated distance) contributions (final state interaction effects). In the decay of ?0 ? 2? ?0and related ones, while involving the one heavy meson in the final state, the phenomenology of the factorization can be described in ?2coefficient which is dominated contribution, so the result may comparable with the experimental one. applying non-perturbative (long- In this work the effective Hamiltonian ????for the ? = 1 transitions is used as 10 ????=?? ?1?1+ ?2?2 ????? ? ????? ? ???? 2 ?=3 31 05 25 6

Amplitudes In the factorization approach, Feynman diagrams for ?0 ? 2? ?0and ?0 ? 2? ?0decays are shown in figure below. Note that if the spectator quarks of d is changed with u in the Feynman diagrams, I can get ?+ ? 2? ?+and ?+ ? 2? ?+decays. 31 05 25 7

Amplitudes There are a current-current and a QCD penguin amplitudes for thesedecay modes, it has been advocated that the new internalW-emission contribution coming from the Cabibbo allowed process? ? ?? ? followed by a conversion of the? ? pair into the ?(2?) via two gluon exchanges is potentially important since its mixing angle ??????(?)is as large as that of the penguin amplitude and yet its Wilsoncoefficient ?2is larger than that of penguin operators. In thecolor-suppressed internal W-emission tree (?2), penguin (?3) and electro-weak penguin (?5, ?7and ?9) diagrams both?0 and ?0mesons are placed in the form factor, the mesonof ?(2?) is produced from the vacuum state, therefore theamplitudes of these decays consist of < ?0 ?0>and< ?0 ?0> multiplied by < 0 ?(2?) > which are factorizable terms. 31 05 25 8

Amplitudes The form factor < ?(??)|??|?(??) > is parametrized as [2] 2 ?? ?2 2 ??+ ?? ? ?? ???1?2 < ? ?? ??? ?? > = 2 ?? ?2 2 +?? ???0?2, where ? = ?,? and ? = ?? ??. The decay constant is defined as [3] > = ??(2?)??(2?)??(2?)?. < 0 ??? 2? ?? 2?,?? 2? ? = 0 the matrix elements of the ?0 Because of ??= ??(2?)?and ??(2?)?.??(2?) ? 2? ?0is given by ? 2? (?3+ ?9+ ?? ?? 2??? 2??1 ] < ? 2? ?0?????0> [?2????? ? ?5+ ?7????? ? ?? 2?.(??+ ??) 2 ???? 2? [2]A.Ali and C. Greub, Phys. Rev. D 57 (1998) 2996. [3]A.Ali, G. Kramer and C.D. Lu, Phys. Rev. D 58 (1998) 094004. 31 05 25 9

Amplitudes The coefficients ??multiplying products of vector currents are renormalization scheme invariant, as are the hadronic matrix elements of these currents. For the coefficients ?5and ?7a scheme dependence remains, which exactly compensates the scheme dependence of the hadronic matrix elements of the pseudoscalar densities associated with these coefficients. These matrix elements are power suppressed by the ratio ??(2?) ??(2?) ? 2?=2??(2?) ?? ?? This equation arise from converting of chiral projection 1 + ?5to 1 ?5by using the Dirac equation, which is formally of order ???/??but numerically close to unity. 31 05 25 10

Amplitudes where ? = ? for ?, ? = ? for K mesons and 2?? ??(2?)| ?| ?? 2?. ??+ ?? = 2?? 2?.??= here | ?| is the absolute value of the 3-momentum of the ? (or the K) in the B rest frame, and [4] ?(0) 2+ ??(?2/?? (???)+?1 ?? (???)+?2? ?? ?1???2= 2)2 1 ???2/?? (???) (???)= ?2 ?2 (???) (???)= ?2? 1 ?2? 1 (? = 2,3,4,5) [4] P. Ball, JHEP 9809 (1998) 005. 31 05 25 11

Amplitudes (???)are the Wilson coefficients evaluated at the renormalization scale ?. These ?? coefficients of the four-Fermi operators depend on the renormalization scale; in addition, in NLO precision, they also depend on the renormalization scheme. These unphysical dependences are compensated in principle by a corresponding scheme/scale dependence of the matrix elements of the operators. The renormalization group evolution from ? ??to ? ??has been evaluated in LO in the electromagnetic coupling and in the NLO precision in the strong ???for the QCD factorization coupling ??[5]. I calculate ??for the naive and ?? approaches. The corresponding simplified amplitudes are given by [5] G. Buchalla,A.J. Buras and M.E. Lautenbacher, Rev. Mod. Phys. 68 (1996) 1125. 31 05 25 12

Amplitudes 2 ??(?? 2? ? 2? ?(?0 ? 2? ?0) = ???? 2??? 2?(?? 2?.??)?1 [?2????? ? ) (?3+ ?9+ ?? ] ?5+ ?7????? ? 2 2???? 2??? 2?(?? 2?.??)?1??(?? 2? [?2????? ? ?(?0 ? 2? ?0) = ) ? 2? ?3+ ?9+ ?? ?5+ ?7????? ? The decay amplitudes for the ?+ ? 2? ?+can be obtained via ? 2? ?0) and for the ?+ ? 2? ?+is the same as ?(?0 ? 2? ?0). 2?(?0 31 05 25 13

Branching Fraction With the factorized decay amplitudes obtained in the previous section, it is ready to compute the decay rates given by [6] ??3 (?0 ? 2? ?0) = 2|?(?0 ? 2? ?0)|2 8??? with 1 2 2 2 ?? 2?+ ?? 2 ?? 2? ?? ??= ?? ?? 2?? The branching ratio can be achieved through ??(?0 ? 2? ?0) = (?0 ? 2? ?0) ??? [6] Z. Xiao, W. Li, L. Guo and G. Lu, Eur. Phys. J. C 18 (2001) 681. 31 05 25 14

Numerical Results The coefficients ??have been calculated in different scheme and scales. In this paper I will use consistently the naive dimensional regularization (NDR) scheme and ? = ??/2, ? = ??and ? = 2??scales. The values of ??at the LO and NLO schemes are shown in table below LO ??(?? ?) ??(?? ?) ?? ?? ?? 0.008 0.004 -0.008 0.023 -0.945 ? = ??/2 0.104 0.002 -0.003 0.067 -0.915 ? = ?? 0.177 0.001 -0.001 0.189 -0.890 ? = 2?? NLO ??(?? ?) 0.062 ??(?? ?) -0.942 ?? 0.084 ?? 0.003 ?? -0.012 ? = ??/2 0.170 0.003 -0.005 0.070 -0915 ? = ?? 0.235 0.002 -0.002 0.186 -0.890 ? = 2?? 31 05 25 15

Numerical Results Branching ratios of B ? 2? ? and B ? 2? ? decays Decay Mode Schemes ? = ??/2 Exp.[1,7] ? = 2?? ? = ?? 0.009 0.000 0.235 0.013 0.620 0.035 1.17 0.17 ( 10 5) LO ?0 ? 2? ?0 0.188 0.011 0.593 0.033 1.067 0.059 NLO 0.018 0.000 0.470 0.026 1.240 0.070 2.44 0.30 ( 10 5) LO ?+ ? 2? ?+ 0.376 0.022 1.186 0.066 2.134 0.118 NLO 0.593 0.032 1.405 0.070 3.691 0.184 6.20 0.50 ( 10 4) LO ?0 ? 2? ?0 1.142 0.058 3.540 0.177 6.344 0.376 NLO 0.593 0.032 1.405 0.070 3.691 0.184 6.39 0.33 ( 10 4) LO ?+ ? 2? ?+ 1.142 0.058 3.540 0.177 6.344 0.376 NLO [1] Belle Collaboration, V. Chobanova, et al, Phys. Rev. D 93 (2016) 031101. [7] J. Beringer et al. (Particle Data Group), Phys. Rev. D 86 (2012) 010001. 31 05 25 16

Conclusion In this research I have calculated the branching ratio of the ?0 ? 2? ?0 ?0 decay by using the factorization approach. I have obtained Br( ? 2? ?0= (1.067 0.059) 10 5 at the NLO scheme and ? = 2?? ) scale. This decay mode, recently have reported by the Belle collaboration, they have obtained Br ?0 ? 2? ?0= (1.17 0.17) 10 5. My result is in good agreement with the Belle collaboration measurement. I have also calculated the same decays of ?+ ? 2? ?+, ?0 ? 2? ?0and ?+ ? 2? ?+in the framework of the naive and QCD factorization method and achieved Br ?+ ? 2? ?+= 2.134 0.118 10 5and Br ?0(+) ? 2? ?0(+)= (6.344 0.367) 10 4. All results are in good agreement with the experimental results. Since the CP-violating asymmetry for ?0 ? 2? ?0decay is not available, the calculations of the last decays were considered for comparison with the main decay in the future. 31 05 25 17

Thank you. 31 05 25 18