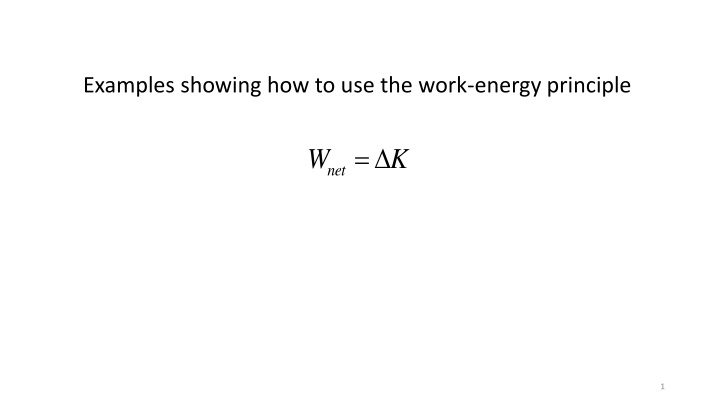Examples Using Work-Energy Principle: Solving Physics Problems
Illustrated examples demonstrate how to apply the work-energy principle in physics problem-solving. Understand the concept of work done, energy transfer, and avoiding kinematics calculations. Learn how to analyze and solve problems efficiently by utilizing the work-energy theorem. Discover practical applications and benefits of this fundamental principle in physics.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Examples showing how to use the work-energy principle = W K net 1
One way it is useful: We can avoid doing kinematics m = 1500 kg = = = = 20 m mg d w F The total work done is: d = 14,700 N 5000 N 36.9 3500 N = W = 10,000J tot o F fr 2
W = 10,000J In the previous example: tot m = = K K W K iv = 0sec Let s assume f i net 1 2 = 2 f 0 W mv net ( 1,500 kg ) 2 W m J 2 10,000 J = = v net = 3.65 f kg 3
2 Nm kg m sec J kg m m sec m sec 2 2 kg kg m fv = 3.65sec we got the answer without using kinematics! 4
m sec iv = 2.0 . Now take same situation, but with = = W K K K net f i 1 2 1 2 = 2 f 2 0 W mv mv net ( 1,500 kg ) 2 2 10,000 J 2 W m m sec = + = + 2 0 v v net 2.0 f m fv 4.2sec Look Mom! No kinematics! 5
Now lets do an example in two different ways: 1. Using kinematics 2. Using the Work-Energy principle 6
Example: Using kinematics iv How far does it go? x fx 0 ix = 0 m Kinematics F = x component y component F = ma = iv = net x F ma 10 m/sec ma net , x , net y y y fx = ? = = F ma 0 F mg F F fr x N N fr fv = 0 m/sec x = F F mg fr k N a = ? = 0.1 k 7
Example: Using kinematics iv How far does it go? x fx 0 F m mg m F = fr = = k a a k m N a = F ma x x x fr x = a g x k = F F fr k N = = F mg 0 F mg N N 8
Example: Using kinematics iv How far does it go? x = fx 0 a g x k Now do kinematics 2 i 2 i v a v ( ) = = x x = + 2 f 2 i 2 v v a x x ( ) f f 2 x f i 2 g x k 2 i v = x f 2 g k ( ) 2 10 m/sec 2 0.1 9.8m/sec fx = 51m fx = = 51m )( ) ( 2 9
Now lets do the same problem, but using work-energy concepts 10
Example: Using the work-energy theorem iv How far does it go? x fx 0 Work-energy theorem W = y K F F net N fr x ( )// = W F d mg net net 11
Example: Using the work-energy theorem iv How far does it go? x fx 0 Work-energy theorem W = y K = F F F net fr net fr x ( )// = W F d net net ( )// = W F d net fr F = kmg )( )cos(180 ) fr ( = o W mg x net k f = d x = W mgx f net k f 12
Example: Using the work-energy theorem iv How far does it go? x fx 0 Work-energy theorem W = 1 2 1 2 = 2 f 2 i K mv mv K We get: net 1 2 ( )// = = 2 i 2 i W F d 0 v K mv = net net x f 2 g k ( )// = W F d net fr = W K net Same result as before! = W mgx 1 2 net k f = 2 i mgx mv k f fx = 51m So, 13
A tractor driving at a constant speed pulls a sled loaded with firewood. There is friction between the sled and the road. The total work done on the sled after it has moved a distance d is A. positive. B. negative. C. zero. D. not enough information given to decide 15
A tractor driving at a constant speed pulls a sled loaded with firewood. There is friction between the sled and the road. The total work done on the sled after it has moved a distance d is A. positive. B. negative. C. zero. D. not enough information given to decide 16
A 6.00-kg block and an 8.00-kg block are connected as shown. When released, the 6.00-kg block accelerates downward and the 8.00-kg block accelerates to the right. After each block has moved 2.00 cm, the force of gravity has done A. more work on the 8.00-kg block than on the 6.00-kg block. B. the same amount of work on both blocks. C. less work on the 8.00-kg block than on the 6.00-kg block. D. not enough information given to decide 17
A 6.00-kg block and an 8.00-kg block are connected as shown. When released, the 6.00-kg block accelerates downward and the 8.00-kg block accelerates to the right. After each block has moved 2.00 cm, the force of gravity has done A. more work on the 8.00-kg block than on the 6.00-kg block. B. the same amount of work on both blocks. C. less work on the 8.00-kg block than on the 6.00-kg block. D. not enough information given to decide 18
A 6.00-kg block and an 8.00-kg block are connected as shown. When released, the 6.00-kg block accelerates downward and the 8.00-kg block accelerates to the right. After each block has moved 2.00 cm, the force of gravity has done A. more work on the 8.00-kg block than on the 6.00-kg block. B. the same amount of work on both blocks. C. less work on the 8.00-kg block than on the 6.00-kg block. D. not enough information given to decide 19
A6.8 Three blocks are connected as shown. The ropes and pulleys are of negligible mass. When released, block C moves downward, block B moves up the ramp, and block A moves to the right. After each block has moved a distance d, the force of gravity has done A. positive work on A, B, and C. B. zero work on A, positive work on B, and negative work on C. C. zero work on A, negative work on B, and positive work on C. D. none of these 20
A6.8 Three blocks are connected as shown. The ropes and pulleys are of negligible mass. When released, block C moves downward, block B moves up the ramp, and block A moves to the right. After each block has moved a distance d, the force of gravity has done A. positive work on A, B, and C. B. zero work on A, positive work on B, and negative work on C. C. zero work on A, negative work on B, and positive work on C. D. none of these 21
And now for potential energy and the conservation of energy 22
Consider gravity h The work done by the gravity force while lifting something straight up is negative mg = = o mgh cos(180 ) W mgh grav The work done by the gravity force while putting it back down is positive mg h = + = o mgh cos(0 ) W mgh grav Work done by the gravity force over the round trip is zero 23
A force is conservative if the work done by that force over a closed path is zero. With conservative forces, you get out what you put in If a force is conservative, then you can define a potential energy function corresponding to that force. Example of a non-conservative force: Friction The work done by friction over a closed path is not zero 0 W In fact, friction You never get back the work done by friction! 24
Consider gravity Lifting something up requires a force from somewhere Dropping something does not So lifting something up is like storing energy in it That s called potential energy Energy that it has, because of its position Potential energy spontaneously converts into kinetic energy unless this is prevented 25
Gravitational potential energy y = U mgh G h = Height of object above the altitude defined to be at zero gravitational PE h Zero gravitational potential energy **You get to choose where the zero GPE altitude is ** You MUST choose where zero GPE is 26
Why is it defined this way? U W It s really defined this way: grav grav h = 0 U W mgh Lifting object: so grav grav mg The object s GPE increases: energy is stored = + 0 U W mgh Putting object down: so mg grav d grav The object s GPE decreases: energy is released 27
So what? = W W If ONLY GRAVITY does work (as when falling), tot grav = K W = work-energy theorem W K grav tot W U Definition of GPE U W grav grav grav grav = K U grav + = 0 K U grav 28
+ = 0 K U grav + E K U Define Total Mechanical Energy: grav 0 E We get: CONSERVATION OF ENERGY!! 29
For Example If ONLY conservative forces (like gravity) do work (as in projectile motion), then the total energy is conserved. Energy conservation means that at any point along the motion, the sum of kinetic and potential energy is a fixed amount The total energy of the object anywhere on the trajectory is the same y ( ) , , sec t x y final f f fy = iv initial E E fv final initial ( ) iy , , 0sec x y i i 0 GPE x fx ix 30
= K U + E Conservation of Energy y + E = K U yi + E = K U 0 GPE + E = K U origin 31
The potential energy function for gravity (near the surface of the earth) is: U mgh h = distance above or below where you choose the zero gravitational potential energy altitude to be. Later: we ll see that the potential energy function for an ideal spring is: 1 2 = 2 U kx spring where is the amount of stretch or compression of the spring x 32
Conservation of energy: = = E E 0 E i f + = + K U K U i i f f y = 0, For the case of gravity, assuming zero GPE is chosen to be at 1 2 1 2 + = + 2 i 2 f mv mgy mv mgy i f 33
Lets re-do this problem: If you release a ball from rest at a certain height above the ground, how fast will it be going just before it hits the ground? y TAKE NOTE OF THE COORDINATE SYSTEM! yi * U=0 34 origin
Lets re-do this problem: If you release a ball from rest at a certain height above the ground, how fast will it be going just before it hits the ground? y Initial position = + E K U i i i yi 1 2 = + 2 i E mv mgy i i iv = 0 m/sec here, = E mgy i i U=0 35 origin
Lets re-do this problem: If you release a ball from rest at a certain height above the ground, how fast will it be going just before it hits the ground? y = + E K U f f f 1 2 = + 2 f E mv mgy yi f f fy = 0 m here, 1 2 = 2 f E mv final position f U=0 36 origin Just before it hits the ground
Only gravity does work, so energy is conserved! = E E i f 1 2 = = = 2 f E mgy mv E y i i f yi U=0 fv origin 37
Only gravity does work, so energy is conserved! = E E i f 1 2 = 2 f mgy mv y i yi U=0 fv origin 38
Only gravity does work, so energy is conserved! = E E i f 1 2 = 2 f mgy mv y i yi = 2 v gy f i This is the same result we got from kinematics! U=0 fv origin 39
Now for some examples 40
Lets re-do this problem: If you release a ball from rest at a certain height above the ground, how fast will it be going just before it hits the ground? y = E E i f = 2 v gy yi f i This is the same result we got from kinematics! U=0 41 origin
Example: mass slides down a frictionless odd-shaped surface initial position yi fv yf 0 final position Try this using and kinematics! F ma = Is energy conserved? Yes: only gravity does work here What about the normal force? It does no work! 42
The normal force is always perpendicular to the direction of motion. So it does no work. 43
Example: mass slides down a frictionless odd-shaped surface initial position yi * fv U=0 0 final position Final Initial = + E K 1 2 U = + E K U f f f i i i = + = + 2 f 0 E mgy 0 E mv i i f 1 2 same result! = = = E E 2 f 2 mgy mv v gy i f f i i 44
Conservation of Energy If only gravity and/or the spring force do work as something moves, then the total mechanical energy is conserved The total mechanical energy is the kinetic energy + the potential energy = K U + E Potential energy Kinetic energy 1 2kx = 1 2 2 U mgh and/or = 2 K mv 45
How to solve conservation of energy problems If only gravity and/or the spring force are the only forces that do work, then the total mechanical energy is conserved. Do this: Draw a picture with a coordinate system Identify an initial and a final position iE Write down an expression for , the total energy in the initial position NOTE: if you use gravitational PE, you must DEFINE where the 0 GPE altitude is Write down an expression for , the total energy in the final position f E Set and solve the problem i f E E = 46
Example 6-8: Rollercoaster car speed using energy conservation Assuming the height of the hill in the figure is 40m, and the rollercoaster car starts from rest at the top, calculate (ignoring friction): (a) The speed of the roller coaster car at the bottom of the hill, and (b) At what height it will have half this speed. y = 40m 47
Example 6-8: Rollercoaster car speed using energy conservation Assuming the height of the hill in the figure is 40m, and the rollercoaster car starts from rest at the top, calculate (ignoring friction): (a) The speed of the roller coaster car at the bottom of the hill, and (b) At what height it will have half this speed. y Conservation of energy initial final y1 = E E i f 1 2 = 2 mgy mv 0 U=0 1 = 2 v gy 1 Final Initial 1 2 1 2 m = + 2 E mv mgy ( ) = + 2 iE mv mgy = 2 9.8 40 m v f f 1 2 sec 1 2 = 2 E mv = iE mgy f m 1 v = 28sec 48
Example 6-8: Rollercoaster car speed using energy conservation Assuming the height of the hill in the figure is 40m, and the rollercoaster car starts from rest at the top, calculate (ignoring friction): (a) The speed of the roller coaster car at the bottom of the hill, and (b) At what height it will have half this speed. final initial You try it! 49
Example 6-8: Rollercoaster car speed using energy conservation Assuming the height of the hill in the figure is 40m, and the rollercoaster car starts from rest at the top, calculate (ignoring friction): (a) The speed of the roller coaster car at the bottom of the hill, and (b) At what height it will have half this speed. y Conservation of energy final initial = E E i f y1 1 2 y2 = + 2 2 mgy mv mgy 1 2 0 U=0 2 2 g v = y y 2 1 2 Final Initial 2 m 14sec 1 2 1 2 = + 2 = + 2 2 iE mv mgy E mv mgy = 40 m y 1 2 f 2 m 2 9.8sec 2 = m iE mgy v = 14sec 1 2 y = 30 m 2 50