Factorising Expressions: Learn How to Factorise Various Terms
In this instructional material, you will learn how to factorise different types of expressions. From expanding a term over a bracket to finding terms that multiply to create an expression, the content covers examples and solutions step-by-step. Explore factorising expressions involving variables like a, b, x, y and understand the process behind simplifying mathematical expressions. Enhance your algebraic skills through practice and clear explanations provided.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
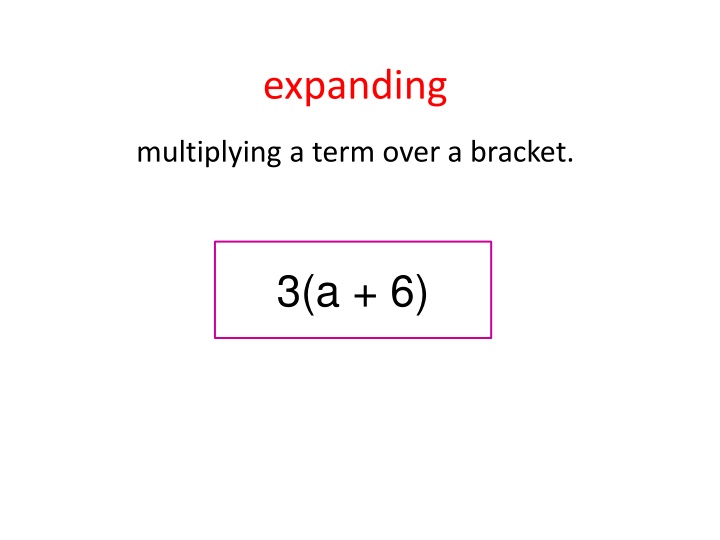
expanding multiplying a term over a bracket. 3(a + 6)
Factorise Finding terms that multiply to make an expression. It is the reverse of expanding. 4a + 3a2
Factorise 15 + 5a 12ab3 + 4a2b
Factorise 4a3 + 10a2b 9a3 + 2b
Factorise 3a2 + 8a3b + 4ab 4xy3+ 6xy
Factorise 6) 6y + 5x2 1) 6a + a2 7) 3ab + 6ab2 2) 12 + 3a 8) 5b2 + 15b 3) 4a2 + 8ab 9) 2a2 + 4a + 6a3 4) 9b + 9b3 10) ab4 + 4ab2 + 3a3b3 5) 4xy2 + 2x2y
answers 1) 6a + a2 = a(6 + a) 6) 6y + 5x2 = N/A 2) 12 + 3a = 3(4 + a) 7) 3ab + 6ab2 3) 4a2 + 8ab = a(6 + a) = 3ab(1 + 2b) 8) 5b2 + 15b 4) 9b + 9b3 = 9b(1 + b) = 5b(b + 3) 9) 2a2 + 4a + 6a3 = 2a(a + 2 + 3a2) 5) 4xy2 + 2x2y = 2xy(y + 2x) 10) ab4 + 4ab2 + 3a3b3 = ab(b3 + 4b + 3a2b2)