Find Odd Out Rectangles & Similar Shapes
Discover which rectangle is the odd one out and explore similar shapes to determine the scale factor of enlargement. Engage in visual challenges to spot similar triangles and understand how shape enlargement affects interior angles.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
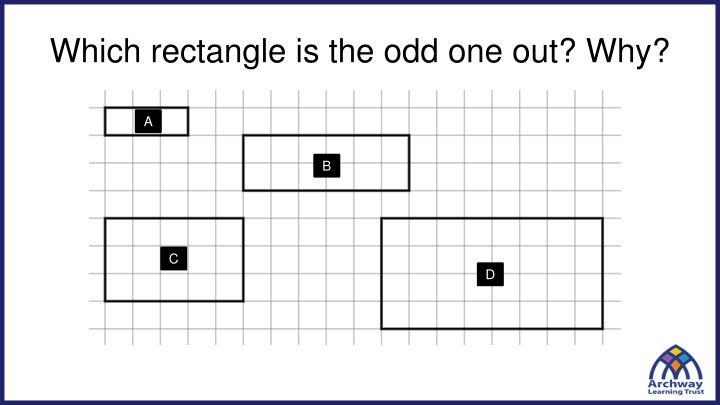
The length is twice the width for rectangles A, B & D If we plotted the dimensions of rectangle C on a conversion graph it would not lie on the line. 12 9 Length 6 3 0 0 1 2 3 4 Width
Rectangles A, B & D are similar A B C D The dimensions of rectangles A, B & D are in proportion
When we enlarge shapes, do the interior angles of the shape change?
When we enlarge shapes, interior angles dont change, only the side lengths. How has each shape been enlarged? Side Lengths 2 Scale Factor of Enlargement: 2 8 metres 4 metres 4 metres 2 metres Side Lengths 3 Scale Factor of Enlargement: 3 6 metres 2 metres 35 35
These are similar shapes. What is the scale factor of enlargement? 6 cm 4 cm 15 cm 8 cm 8 4= 2 15 6= 5 2= 2.5
These are similar shapes. What is the scale factor of enlargement? 4 cm 3 cm 12 cm 15 cm 12 4= 3 15 3= 5
These are pairs of similar shapes. Find the scale factor of enlargement for each pair. These are similar shapes. What is the scale factor of enlargement? 12 cm 6 cm 2 A 3 cm 14 cm 2 cm B 7 15 cm 2.5 C 3.5 D 15 3= 5 1.2 6 cm 5 cm E
Can you spot the two similar triangles? 12m 4m 5m 15m
Can you spot the two similar triangles? Sketch them
Sketch out the similar triangles for each diagram. Work out the missing lengths.
Are these shapes similar? 8 cm 4 cm 8 cm 14 cm 8 4= 2 We can compare corresponding sides. 7 4= 14 8= The length has 1.75 a smaller scale factor of enlargement than the width. The shapes are not similar.
Are these shapes similar? 20 cm 10 cm 6 cm 25 cm 25 10= 2.5 We can compare corresponding sides. 20 6= 10 3= The width has 3.33 a larger scale factor of enlargement than the length. The shapes are not similar.
Compare corresponding sides to check whether these pairs of shapes are similar. 6 cm 3 cm 8 cm 12 cm 3 cm 18 cm 9 cm A B SF = 3 5 cm 5 cm 15 cm 24 cm 15 cm 37.5 cm 8 cm C D SF = 2.5 SF = 1.6
