FLASH Technical Design Report: Signal Amplification and Acquisition for MSA
This report focuses on the Signal Amplification and Acquisition for the Microstrip SQUID Amplifier (MSA) in the FLASH project. It outlines the operational constraints, objectives, tasks, and configurations related to optimizing the MSA for optimal noise temperature. The report details the frequency ranges, magnetic field operation, temperature requirements, and noise contributions, emphasizing the importance of negligible noise compared to thermal noise. It also highlights the measurements, stability, post-amplification, shielding, multiplexing, digitization, and testing involved in the MSA implementation.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
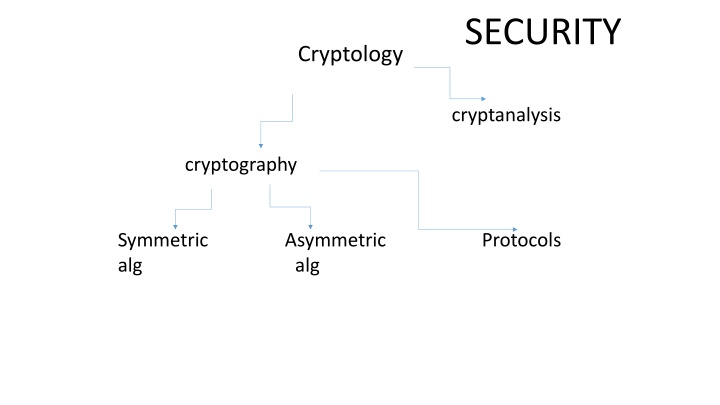
SECURITY Cryptology cryptanalysis cryptography Symmetric Asymmetric Protocols alg alg
m = plaintext message c = ciphertext k = secret key E,D = cipher Alice & Bob are talking Eve is always listening Bob Alice c E(k,m) = c D(k,c) = m m D E k k Eve
One-time vs many time key Symmetric vs asymmetric E(x) = D(x)
SECURITY Cryptology cryptanalysis cryptography Symmetric Asymmetric Protocols alg alg
SECURITY Cryptology cryptanalysis cryptography Symmetric Asymmetric Protocols Stream block Ciphers ciphers
Stream Ciphers on the fly
Key bits Key bits s4, s3, s2, s1, s0 s4, s3, s2, s1, s0 voice bits y4, y3, y2, y1, y0 cyphertext voice bits x4, x3, x2, x1, x0 x4, x3, x2, x1, x0 cleartext cleartext
how does a voice turn into bits? (another example of digitizing (thanks to Claude)) voice bits x4, x3, x2, x1, x0 cleartext -- https://discover.hubpages.com/technology/Microphones
Stream cipher works bit by bit E(Yi) = (yi + si) mod 2 - this is the encryption algorithm D(Xi) = (xi + si) mod 2 - this is the decryption algorithm voice bits key bits Why are they the same? Why not minus for decryption?
XOR exclusive or What your mom probably means when she asks if you want vanilla ice cream or strawberry ice cream X Y X xor Y ------------------------------ 0 0 0 0 1 1 1 0 1 1 1 0 One or the other, but not both Xor is its own inverse
as opposed to inclusive or: X Y X xor Y ------------------------------ 0 0 0 0 1 1 1 0 1 1 1 1
Addition and subtraction are the same operation 0-0 = 0 1-0 = 1 0-1 = 1 1-1 = 0 0+0 = 0 0+1 = 1 1+0 = 1 1+1 = 0 Key bits Key bits s4, s3, s2, s1, s0 s4, s3, s2, s1, s0 y4, y3, y2, y1, y0 cyphertext x4, x3, x2, x1, x0 x4, x3, x2, x1, x0 cleartext cleartext
Clear message key bit cypher bits key bit clear message bit options options bit recovered M K E K D -------------------------------------- 0 0 0 0 0 1 1 1 0 Two possible message bits Two possible key bits M K E K D -------------------------------------- 1 0 1 0 1 1 0 1 1
resulting cypher bits possible key bits Xi Si Yi = Xi Si ------------------------------------------------------------------------------------------------ 0 0 0 0 1 1 possible message bits In both cases each plaintext bit can become either 0 or 1 1 0 1 1 1 0 I.E. -. Key bit == 0, m stays the same Key bit == 1, m flips
Xor is its own inverse A B A xor B (A xor B) xor A (A xor B) xor B -------------------------------------------------------------------------------------------------- 0 0 0 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1
If Key bit is a zero, stay the same If key bit is a one, flip it So it comes down to where are the 1 s in the key stream ? If the key stream is 1 s and 0 s, then of the ciphertext bits are in clear text
There should be no discernible pattern in the key stream Where are the 1 s, and where are the 0 s ? How should we decide?
Random number generation Pi, e, division, is the universe discrete? social use, media use of the term random is usually far away from what this guy had in mind:
For us: 3 classes of random number generation 1. True random number generators TRNG True random numbers come from physical processes (random process or just not-understood?)
Coin flipping, lottery, dice, roulette, thermal noise, timing, mouse movement disk speed variance, radioactive decay (but humans are terrible) hard to integrate into your program, maybe use mturk Truly random you can t recreate them, they can be slow
2. Pseudo random number generators PRNG The distribution of the values is uniform, but they are computed/deterministic S0 = seed Si+1 = f(Si)
rand function in c, srand, drand, drand48, Java stuff: S0 = 12345 Si+1 = (1103515245 * Si + 12345) % 231
3. Cryptographically secure pseudo random number generator - CPRNG PRNG with the following property: generated values are unpredictable (unlike drand48, inter alia) which means that if I give you N output bits it is not computationally feasible to compute the next one
There are many applications where you need random numbers PRNG s are well understood and almost always suitable for you application Except for cryptography applications, where they are unusable
So, how can we generate the key bits? k k PRNG PRNG y4, y3, y2, y1, y0 x4, x3, x2, x1, x0 x4, x3, x2, x1, x0
Addition and subtraction are the same operation K = a,b What s in LCG ? K = a,b LCG LCG (Linear congruential generator) y4, y3, y2, y1, y0 x4, x3, x2, x1, x0 x4, x3, x2, x1, x0
We are going to build a gadget to generate the key bits. It has to be small enough to fit in your cell phone, use only a tiny amount of power (== battery life), and generate very little heat First though, we need some background
shift registers logic gates how we remember a bit
Flip-Flops also called a latch (i.e memory) S Q Q' R Asynchronous feedback paths -instability operates with both inputs normally at 1 application of a momentary '0' to the S(et) input causes Q to go to 1 and Q' to go to 0 application of a momentary '0' to the R(eset) input causes Q to go to 0 and Q' to go to 1
block diagram for a flip-flop/ latch 1 in out it always holds either a 0 or a 1 when the clock ticks, the input will be stored next and the output will flow to the input of another
We are going to connect these flip-flops in series. The output of one is connected to the input on the next. Each time the clock ticks, the bit moves one position to the right 1 0 1 0 0 1 . . . 0 1 1 this piece of hardware is called a the bits which fall out at the end are the key bits which we will use to encrypt the voice bits register (where all the action happens)