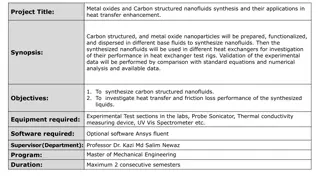
Fourier's Law in Heat Transfer
Fourier's Law provides a rate equation for conduction heat flux, determining thermal conductivity and temperature distribution. Explore its applications, implications, and the heat equation in various coordinate systems for solving heat transfer problems.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
ME 345 Heat Transfer (HTx) Professor: Dr. Dan Cordon (AKA Dr. Dan)
FOURIERS LAW A rate equation that solves for the conduction heat flux from a known temperature distribution. Its most general (vector) form for multidimensional conduction is: ? = ? ? Implications: Heat transfer is in the direction of decreasing temperature (basis for minus sign) Fourier s law serves to define the thermal conductivity of the medium Direction of heat transfer is perpendicular to lines of constant temperature (isotherms). Heat flux vector may be resolved into orthogonal components.
FOURIERS LAW Application Questions: If the hot and cold sides were flipped, does that change the rate of heat transfer through the solid? Does the value of thermal conductivity change the steady-state temperature distribution through the wall? What parameters can you alter to change the rate of heat passing through a solid via conduction?
FOURIERS LAW Space Shuttle ceramic, heat soaked in oven at 2200 degrees F. Just removed from oven (still glowing) seconds prior.
FOURIERS LAW Poor Decision? Why? Or Why Not?
THE HEAT EQUATION Fourier s Law allows us to calculate a heat flux from a known temperature distribution. Often we don t know the temperature distribution. We use the heat equation to relate boundary and initial conditions (along with geometries and material properties) to calculate a temperature distribution. Use a differential control volume, and apply conservation of energy Result is a differential equation Using known boundary conditions and initial conditions this can be solved to determine the temperature distribution
The HEAT EQUATION Cartesian Coordinates Consider homogeneous medium and taking a differential chunk from it. The heat rate at each surface: The energy generation rate: The energy storage rate:
The HEAT EQUATION Cartesian Coordinates The general form of conservation of energy is Substituting in the terms from previous slide And substituting in equations for the x+dx, y+dy, and z+dz terms Remembering Fourier s Law for heat rates (qx, qy, and qz)
The HEAT EQUATION Cartesian Coordinates Substitute Fourier s Law terms to get the general form of the Heat Equation in cartesian coordinates When you solve this equation you get the full complete temperature distribution T(x, y, z) as a function of time! Each term is just part of the conservation of energy equation. For instance, is related to the net heat rate into the control volume (qx qx+dx) via conduction.
The HEAT EQUATION Cartesian Coordinates A simpler form of equation 2.17 comes from assuming thermal conductivity is constant In the equation above, is called thermal diffusivity. Another simpler form is for Steady-State, where equation 2.17 becomes
The HEAT EQUATION Cylindrical Coordinates A similar set of equations exists for the Heat Equation in cylindrical coordinates
The HEAT EQUATION Spherical Coordinates A similar set of equations exists for the Heat Equation in spherical coordinates
THE HEAT EQUATION Okay now what? Eventually we will be solving the Heat Equation as a way to find the temperature distribution. In this class we will explore simpler cases (1D, maybe some 2D, often steady-state). In graduate classes you will be able to solve (or simulate) 3D transient problems. Let s do some calculations assuming we know the temperature distribution in the solid
Example Problem 2.2 At a certain instant in time the 1D temperature distribution through a 1 [m] thick wall is: Find: 1. Rate of heat transfer entering the wall (at x = 0), and leaving the wall (x = 1 [m]) 2. Rate of change of energy storage in the wall 3. Time rate of temperature change at a. x = 0 b. x = 0.25 [m] c. x = 0.5 [m]
Example Problem 2.2 Assumptions: 1D temperature distribution (only changing in x) Properties are uniform throughout the wall Properties are not changing with temperature (or time) Heat generation term is uniform over entire volume Plan (Part 1) Rate of heat transfer can be found using Fourier s Law (since we already know the temperature distribution)
Example Problem 2.2 Part 1
Example Problem 2.2 Plan (Part 2) Rate of change of energy storage in the wall will come from the overall conservation of energy equation. We just found the energy coming in and the energy leaving. If we solve for the energy generation we have everything we need.
Example Problem 2.2 Plan (Part 3) Time rate of temperature change is a little trickier. But we can get it by rearranging the Heat Equation. Evaluate the derivatives: Note: above result is independent of position!
Example Problem 2.2 Plan (Part 3) Looking at our equation for time rate of temperature change None of the terms above depend on position. For this problem the time rate of change in the wall is the same everywhere! Substitute in values: