Geometry Concepts: Circumference, Arc Length, and Areas Explained
Explore the fundamental concepts of Circumference, Arc Length, and Areas in geometry. Learn how to calculate them, round to the nearest units, and find exact measurements in various scenarios. Enhance your understanding of geometric principles with practical examples and explanations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
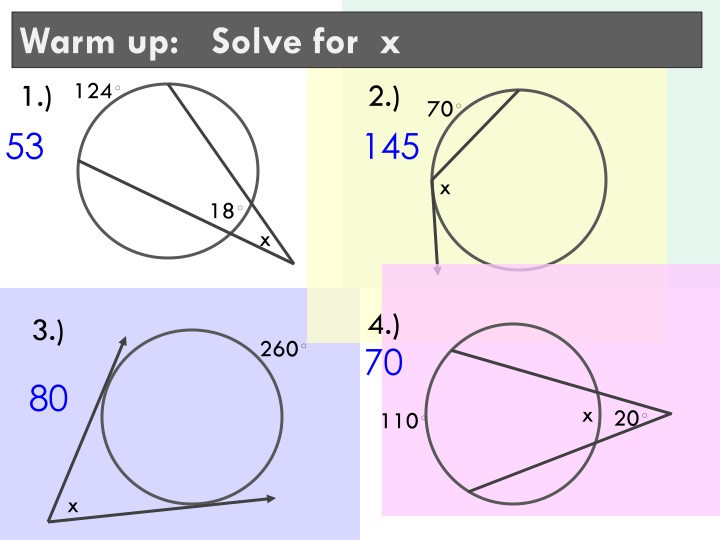
Warm up: Solve for x 1.) 53 124 2.) 145 70 x 18 x 4.) 70 3.) 260 80 20 x 110 x
EOC REVIEW Question of the Day
Circumference, Arc Length, Area, and Area of Sectors
Circumference The distance around a circle
Circumference Twinkle, Twinkle Little Star Circumference Equals 2 pi r C C 2 r d = = or
2 Types of Answers Exact Pi will be in your answer Rounded Type the Pi button on your calculator Toggle your answer Do NOT write Pi in your answer
Find the EXACT circumference. ( ) C 2 14 = 1. r = 14 feet C 28 ft = 2. d = 15 miles ( ) C 15 = C 15 miles =
Ex 3 and 4: Find the circumference. Round to the nearest tenths. 14.3 mm 33 yd ( ) ( ) C 2 14.3 = C 33 = C = 89.8 mm C = 103.7 yd
Arc Length The distance along the curved line making the arc (NOT a degree amount)
Arc Length measure of arc 360 = 2 Arc Length r
Ex 5. Find the Arc Length Round to the nearest hundredths measure of arc 360 = 2 Arc Length r 8m 70 360 ( ) 8 = 2 Arc Length 70 Arc Length 9.7 = 7 m
Ex 6. Find the exact Arc Length. measure of arc 360 = 2 Arc Length r 120 360 ( ) 5 = 2 Arc Length 10 3 Arc Length = in
Ex 7. What happens to the arc length if the radius were to be doubled? Halved? measure of arc 360 = 2 Arc Length r 20 3 Doubled 5 Halved 3
Ex 8. Find the perimeter of the region. 30 9 units +
Area of Circles The amount of space occupied. A = r2 r
Find the EXACT area. ( ) 2 A 29 = 8. r = 29 feet 2 A 841 ft = 2 44 2 9. d = 44 miles A = 2 A 484 mi =
10 and 11 Find the area. Round to the nearest tenths. 53 cm 7.6 yd 2 53 2 ( ) 2 A 7.6 = A = 2 A = 181.5 yd 2 A = 2206.2 cm
Area of a Sector the region bounded by two radii of the circle and their intercepted arc.
Area of a Sector measure of arc 360 2 = A r
Find the area of the sector to the nearest hundredths. Example 12 R 60 360 ( ) 6 2 = A 60 Q A 18.85 cm2
Example 13 Find the exact area of the sector. 6 cm 120 360 ( ) 7 7 cm 2 = A R Q 120 49 2 A cm = 3
Area of minor segment = Example 14 (Area of sector) (Area of triangle) 1 2 mRQ 2 Area of minor segment = r b h R 360 90 360 1 2 (12) 2 = (12)(12) Q 12 yd =113.10 72 2 Area of minor segment =41.10yd
Textbook p. 411 #2 14