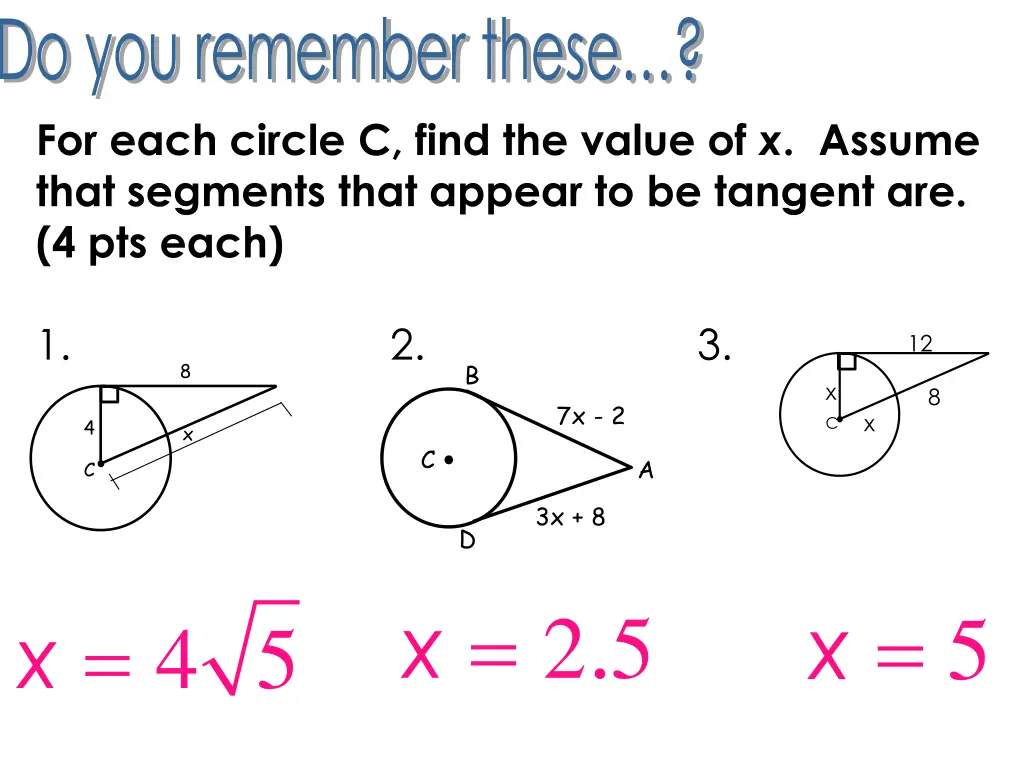
Geometry Practice Questions and Concepts Explained
Practice solving geometry problems involving circles and spheres, including finding values of x in tangent circles, surface area, volume calculations, and properties of spheres. Understand concepts such as great circles, hemispheres, radius, circumference, and more.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Do you remember these? For each circle C, find the value of x. Assume that segments that appear to be tangent are. (4 pts each) 1. 2. 3. 12 x 8 x C x = 2 5 . x = 5 x = 4 5
EOC Practice Question of the Day
Surface Area & Volume of Spheres
If you cut a sphere right down the middle you would create two congruent halves called HEMISPHERES. You can think of Earth. The equator cuts Earth into the northern and southern hemisphere.
Look at the cross section formed when you cut a sphere in half. What shape is it? A circle!!! This is called the GREAT CIRCLE of the sphere.
Surface Area of a Sphere SA = 2 4 r
Surface Area of a Sphere (round to the nearest hundredths) 2 SA 4 r = 8 in 2 SA 4 8 = 2 SA 804 25 in = .
Surface Area of a Sphere (round to the nearest hundredths) 2 SA 4 r = 10 cm 2 SA 4 5 = 2 SA 314 16 cm = .
Volume of a Sphere 4 3 3 V r =
Volume of a Sphere 4 3 3 V r = (round to the nearest hundredths) 4 3 ( ) 2 3 2 cm V = 3 V 33 51 cm = .
Volume of a Sphere 4 3 (round to the nearest hundredths) 3 V r = 10 cm 4 3 ( ) 5 3 V = 3 V 523 60 cm = .
The circumference of a great circle of a sphere is 25 inches. Find the volume of the sphere. (Round to the nearest hundredths.) C 25 r = 2 2 r r = = . 3 979 ) 3 979 25 in 4 3 ( 3 V = . 3 V 263 88 in = .
Ratio Relationships a:b Ratio of the scale factor a:bRatio of the corresponding sides a:b Ratio of the perimeters a2:b2 Ratio of the area a3:b3 Ratio of the volume
Volume of a Sphere A spherical balloon has an initial radius of 5 in. When more air is added, the radius becomes 10 in. Explain how the volume changes as the radius changes. 3 4 3 V r = 10 in 5 in 3 V 4188 8 in = . 3 V 523 6 in = . 5:10 or 1:2. So 13:23means the volume would be 8 times as much.
Volume of a Sphere A sphere has an initial volume of 400 cm.3 The sphere is made bigger by making the radius 4 times as big. What is the new volume of the sphere? 1:4 So, 13:43means the volume would be 64 times more volume. 64 times 400 = 25 600 cm V = 3 ,
Volume of a Sphere A sphere is inscribed in a cube-shaped box as pictured below. To the nearest centimeter, what is the volume of the empty space in the box? ( ) 8 3 4 3 sphere V = 10 in ( ) 3 cube V 16 = 4 3 ( ) 8 3 3 16 cm. empty space V 16 = 1951 cm = 3 empty space V
Homework Practice Worksheet #29 find volume only






















