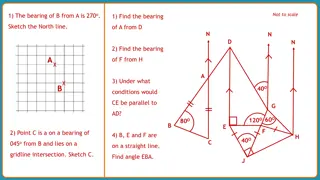
Geometry Trig Parallel Lines and Angles Practice Pages
Enhance your understanding of angles and parallel lines with practice exercises on identifying angle pairs, justifying relationships, and solving algebraic problems. Dive into the world of geometry and trigonometry through these engaging activities.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
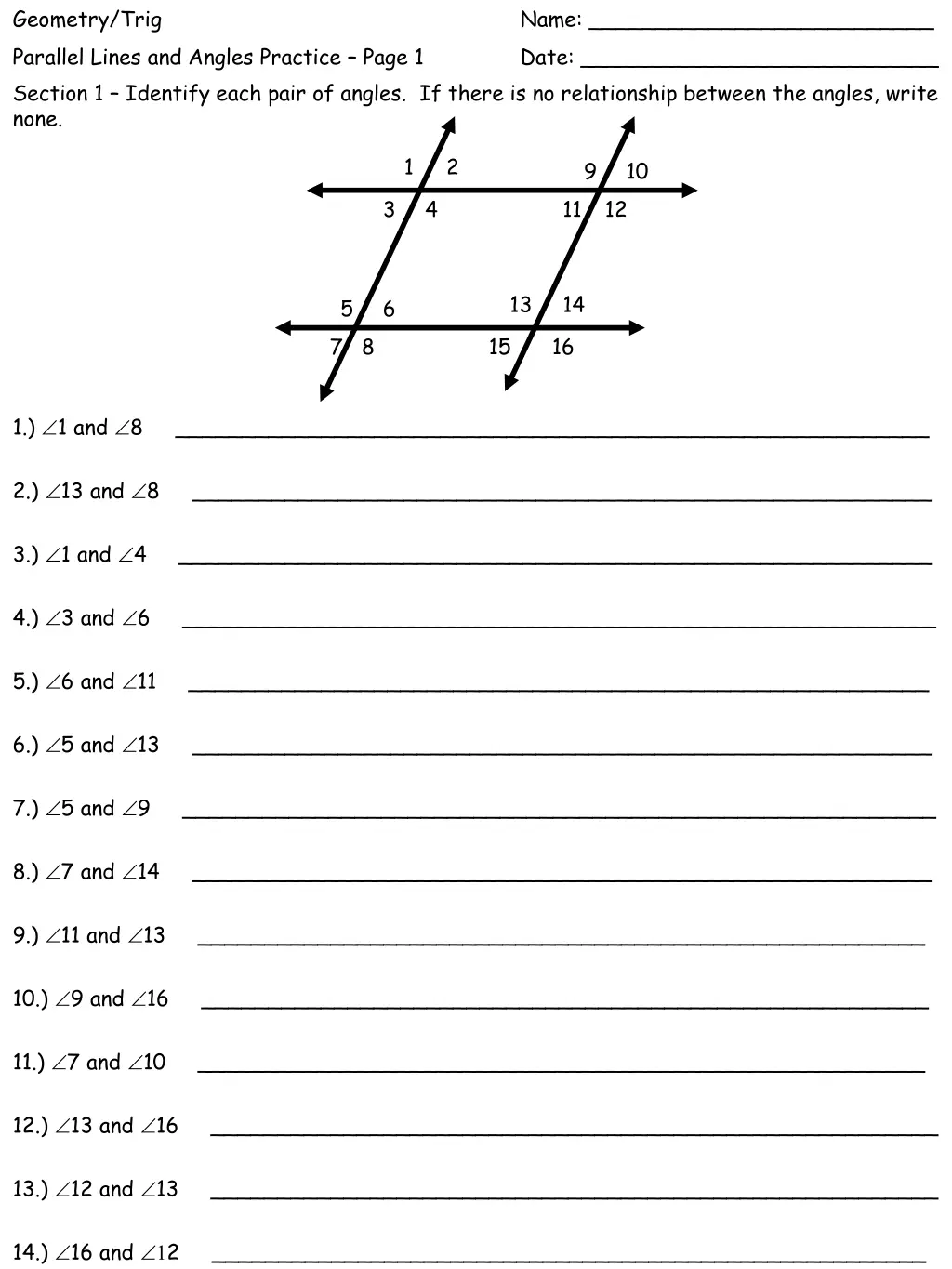
Geometry/Trig Parallel Lines and Angles Practice Page 1 Section 1 Identify each pair of angles. If there is no relationship between the angles, write none. Name: __________________________ Date: ___________________________ 1 2 9 10 3 4 11 12 13 14 5 6 7 8 15 16 1.) 1 and 8 _________________________________________________________ 2.) 13 and 8 ________________________________________________________ 3.) 1 and 4 _________________________________________________________ 4.) 3 and 6 _________________________________________________________ 5.) 6 and 11 ________________________________________________________ 6.) 5 and 13 ________________________________________________________ 7.) 5 and 9 _________________________________________________________ 8.) 7 and 14 ________________________________________________________ 9.) 11 and 13 _______________________________________________________ 10.) 9 and 16 _______________________________________________________ 11.) 7 and 10 _______________________________________________________ 12.) 13 and 16 _______________________________________________________ 13.) 12 and 13 _______________________________________________________ 14.) 16 and 2 ______________________________________________________
Parallel Lines and Angles Practice Page 2 Part 2 Use the diagram below to complete each exercise. All justifications must be written in a formal matter. Example It would be unacceptable to write Corresponding s are . You must instead write, If lines are parallel, then corresponding angles are congruent. 1.) 3 7 Justification: _________________________________ ______________________________________________ ______________________________________________ ______________________________________________ a // b 1 2 b 3 4 2.) 3 and 5 are supplementary 5 6 a 7 8 Justification: ___________________________________ ______________________________________________ ______________________________________________ ______________________________________________ 3.) 4 5 Justification: ___________________________________________________________ _____________________________________________________________________. 4.) 1 8 Justification: ___________________________________________________________ _____________________________________________________________________. 5.) m 7 + m 8 = 180 Justification: ___________________________________________________________ _____________________________________________________________________. 6.) 5 8 Justification: ___________________________________________________________ _____________________________________________________________________. 7.) 2 and 8 are supplementary Justification: ___________________________________________________________ _____________________________________________________________________.
Parallel Lines and Angles Practice Page 3 Part 3 Use the diagram to complete each algebra connection problem. You must show all work. 1. m 1 = x +3 and m 5 = 2x 20. a // b 1 2 What type of angles are they? _________________________ Congruent or supplementary? __________________________ b 3 4 5 6 a 7 8 x = ________ m 1 = _______ m 5 = ________ m 6 = ___________ m 8 = __________ 2. 3. m 3 = 56 and m 6 = 2x 4. m 2 = 3x 10 and m 7 = 2x + 16 What type of angles are they? _________________ Congruent or supplementary? __________________ What type of angles are they? _________________ Congruent or supplementary? __________________ x = ______ x = ______ m 3 = _________ m 6 = ________ m 2 = _________ m 7 = ________ m 5 = _________ m 7 = ________ m 1 = _________ m 4 = ________ 4. 5. What type of angles are they? _________________ Congruent or supplementary? __________________ m 4 = 3x 8 and m 6 = x 4 What type of angles are they? _________________ Congruent or supplementary? __________________ m 1 = 2x 6 and m 7 = x - 3 x = ______ x = ______ m 4 = _________ m 6 = ________ m 1 = _________ m 7 = ________ m 7 = _________ m 8 = ________ m 5 = _________ m 6 = ________
Geometry/Trig Practice: What two lines are parallel (if any) according to the given information? Name: _________________________ n REASONS: A. If corresponding angles are congruent, then lines are parallel. l m 17 11 10 12 18 j B. If alternate interior angles are congruent, then lines are parallel. 9 8 14 6 13 C. If alternate exterior angles are congruent, then lines are parallel. 2 1 4 5 3 D. If same side interior angles are supplementary, then lines are parallel. k 1920 7 15 16 E. If same side exterior angles are supplementary, then lines are parallel. GIVEN Parallel Lines Reason Ex. m 7 = m 8 j // k A 1. m 7 = m 4 ___________ ___________ 2. m 5 + m 6= 180 ___________ ___________ 3. m 8 = m 1 ___________ ___________ 4. m 10 + m 7= 180 ___________ ___________ 5. m 1 = m 7 ___________ ___________ 6. m 8 + (m 2 + m 3)= 180 ___________ ___________ 7. m 1 = m 4 ___________ ___________ 8. m 1 + m 2 + m 3= 180 ___________ ___________ 9. m 17 = m 20 ___________ ___________ 10. m 3 = m 14 ___________ ___________ 11. m 2 = m 13 ___________ ___________ 12. m 11 = m 16 ___________ ___________
Geometry/Trig USING Parallel Line Proofs Page 1 Name: _________________________ Date: __________________________ 1. Given: g // h and s // t Prove: 2 15 1 9 2 10 g 11 12 3 4 5 6 13 14 h 15 16 7 8 t s Statements Reasons 2. Given: k // m Prove: 1 is supplementary to 7 2 6 m 1 5 4 8 k 3 7 t Statements Reasons
USING Parallel Line Proofs Page 2 3. Given: CD // BE; 3 1 Prove: BE bisects DBA C B 3 2 1 A D E Statements Reasons 4. Given: AD // BC; 1 2 Prove: AB bisects CAD C 2 1 A B 3 Statements Reasons D
PROVING Parallel Line Proofs Page 3 5. Given: 4 13; t // s Prove: h // g 1 9 10 2 g 3 4 11 12 5 6 13 14 h 7 8 15 16 t s Statements Reasons 6. Given: AB bisects CAD; 1 2 Prove: AD // BC C 2 1 A B 3 Statements Reasons D
PROVING Parallel Line Proofs Page 4 7. Given: 1 8 Prove: 5 7 2 6 m 1 5 4 8 3 7 k Statements t Reasons 8. Given: c // d; 1 and 14 are supplementary Prove: a // b 9 10 1 2 a 11 12 3 4 13 14 5 6 b 15 16 7 8 Statements c d Reasons
Parallel Line Proofs Page 5 9. Given: AB // CD; 2 6 Prove: BC // DE B D 2 6 34 5 7 1 A C E Statements Reasons 10. Given: BC // DE; 2 6 Prove: AB // CD B D 2 6 34 5 7 1 A C E Statements Reasons
Parallel Line Proofs Page 6 C 11. Given: BE bisects DBA; 3 1 Prove: CD // BE B 3 2 1 A D E Statements Reasons P R 12. Given: 1 2; 4 5 Prove: 3 6 HINT: First prove PQ // RS, then you should just need one more step to get to this prove. 3 4 T 2 5 6 S 1 Statements Reasons Q