Graphs and Trees: Understanding Relationships in Graph Theory

In the world of graph theory, graphs and trees play a significant role in describing relationships among items in a collection. Graphs consist of vertices representing intersections or stations, connected by edges like roadways or friendships. Trees, on the other hand, are minimally connected graphs with no cycles, making each vertex connected without any loops. Discover the properties of trees, the structure of rooted trees, and the distinction between rooted and unrooted trees. Dive into the fascinating realm of graphs and trees to understand the intricate connections that shape various data structures.

• Graph Theory
• Relationships
• Vertices
• Edges
• Trees

ethington_d Follow

Uploaded on Feb 25, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. CMPT 706 - Algorithms for Big Data Graphs February 13, 2020 Graphs 1-1

2. Graphs Graphs 1-2

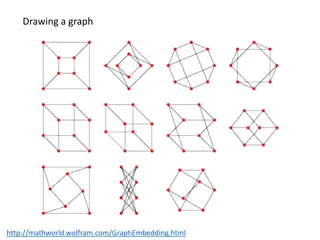
3. Graphs A graph describes relationships among items in a collection - the items are the vertices (depicted by dots or junctions) - the relations are the edges (depicted by lines between dots) What are the vertices and edges in these common graphs? Vertices - intersections Edges - roadways Edges - pipes Edges - friendships Vertices - stations Vertices - people Graphs 1-3

4. Trees Graphs 1-4

5. Trees A tree is a minimally connected graph. all vertices connected no cycles Graphs 1-5

6. Trees Graphs 1-6

7. Trees Graphs 1-7

8. A tree Graphs 1-8

9. Not a tree Graphs 1-9

10. More trees Each of the connected components below is a tree Graphs 1-10

11. A forest A forest is a simple graph with no cycles (not necessarily connected). Graphs 1-11

12. Properties of trees For a connected graph G=(V,E) the following are equivalent 1) G is a tree 2) for any two vertices a b there is a unique path from a to b. 3) |E|=|V|-1 Graphs 1-12

13. Structure of rooted trees Root Leaves Graphs 1-13

14. Structure of rooted trees Parent Vertex/node Children Graphs 1-14

15. Rooted vs Unrooted trees An unrooted tree can be turned into a rooted tree by choosing a root, and directing all edges away from the root. a e f g c b c a g f a c d b d e d e b f g a is the root e is the root Graphs 1-15

16. More terminology Let T=(V,E) be a rooted tree with root r. Fix some vertex u Any vertex on the path from the root to u is an ancestor of u. Any vertex below (child or child of a child ) u is a descendant of u. An internal vertex is a vertex that has at least one child. A subtree rooted at the subgraph of a tree induced by u and all its descendants. Graphs 1-16

17. More terminology For the tree below find: All children of c? Parent of b? Ancestors of f? All descendant of a? All leaves/Terminal vertices? All internal vertices? a b c d g e f Graphs 1-17

18. Exploring graphs Graphs 1-18

19. Exploring a tree Input: A tree T=(V,E) and a vertex v Goal: explore all vertices reachable from v Explore(T, root) 1. pre_visit(root) // e.g. print( visited root) 2. for each child of u, i.e., every edge (root,u) do 21. Explore (T, u) 3. post_visit(root) // e.g. print( done with root) Q: What is the runtime of the algorithm? What about traversing a general graph? Graphs 1-19

20. Depth First Search (DFS) Create clock starting with 0. Input: A graph G=(V,E) and a vertex v Goal: explore all vertices reachable from v Explore(G, v) 1. set v.visited=true 2. pre_visit(v) // e.g. print( done with v) 3. for all neighbours u of v do 3.1 If u.visited = false Explore (G, u) 4. post_visit(v) // e.g. print( done with v) pre_visit(v): clock++ v.pre = clock post_visit(v): clock++ v.post = clock Q: What is the runtime of the algorithm? Graphs 1-20

21. Depth First Search (DFS) 1 /16 a a /15 /11 2 10 b c b c 6 /9 3 /14 d e f /12 d e f 5 g h 7 /8 g h 4 / 13 previsit postvisit Explore(G,a) DFS tree Graphs 1-21

22. DFS finding connected components Types of edges of a graph for a given DFS: Given a directed graph G=(V,E) we have 4 types of edges Tree edges the edges that belong to the DFS tree Forward edges edges going from a node in DFS tree to its descendant Back edges - edges going from a node in DFS tree to its ancestor Cross edges all other edges. Graphs 1-22

23. DFS finding connected components Input: An undirected graph G=(V,E) Goal: find all connected components of G DFS(G, v) 1. For all vertices v set v.visited = false set v.CC = 0 // v.CC=5: v belongs to the 5th connected component 2. C = 1; // counter for connected components 3. For all vertices v if v.visited = false explore(G,v,C) C = C+1 Explore: inside previsit set v.CC=C Graphs 1-23

24. Strongly connected components in directed graphs Graphs 1-24

25. Strongly connected components Let G=(V,E) be a directed graph. Two vertices u,v are connected if there a path from u to v and from v to u. Equivalently there is a cycle containing both u and v. A directed graph is said to be strongly connected if there is a path from any vertex to any other vertex. A set W of vertices is a strongly connected component if it is a maximal subset of the vertices such that any two of them are connected. Graphs 1-25

26. Strongly connected components Let G=(V,E) be a directed graph. The meta-graph of G is the directed graph of strongly connected components. Observation: the meta-graph is a DAG directed acyclic graph Graphs 1-26

27. Directed Acyclic Graphs (DAG) Consider a DFS for a DAG. Observation 1: A DAG contains no cycles its DFS has no back edges. Observation 2: for every edge u->v we have u.post > v.post Observation 3: Sorting the vertices according to their post number gives a topological order order where all edges are left to right. Graphs 1-27

28. Finding strongly connected components Let G=(V,E) be a directed graph. The meta-graph of G is the directed graph of strongly connected components. Claim 1. When running DFS from any node v, DFS visits exactly all vertices reachable from v. Claim 2. The node that receives the highest post number in DFS belongs to a source of the meta-graph. Claim 3. Let ? and ? be strongly connected components. If there is an edge from a vertex from ? to a vertex from ?, then the highest post number in ? is higher than the highest post number in ?. Graphs 1-28

29. Finding strongly connected components Input: A directed graph G=(V,E) Output: All strongly connected components of G. GR the graph G with all edges reversed Algorithm(G) 1. Run DFS on GR, and sort the vertices by their post number 2. Take v with the highest post number and run DFS(G, v) All vertices reachable from v are the connected component of v. 3. Remove CC(v) from G, and return to step 2 Graphs 1-29

30. Homework and Reading for next time Exercises from the Book: 3.1, 3.2, 3.3, 3.4 Reading 3.1, 3.2, 3.3, 3.4 Graphs 1-30