Graphs of Tangent & Cotangent
Graphs of the tangent and cotangent functions, their transformations, periods, domains, ranges, and asymptotes. Understand how to graph them using the unit circle, find vertical asymptotes, and apply vertical and horizontal shifts to the functions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
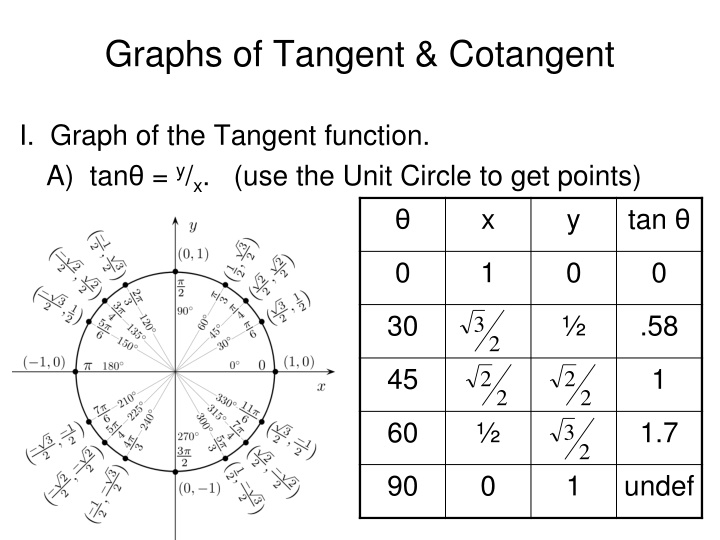
Graphs of Tangent & Cotangent I. Graph of the Tangent function. A) tan = y/x. (use the Unit Circle to get points) x y tan 0 1 0 0 30 .58 3 2 45 1 2 2 2 2 60 1.7 3 2 90 0 1 undef
Graphs of Tangent & Cotangent I. Graph of the Tangent function. B) Graph is
Graphs of Tangent & Cotangent II. Graph of the Cotangent function. 1 = A) Since cot is the reciprocal of tangent cot tan y and tan = x x then cot = y B) Graph of cot is
Graphs of Tangent & Cotangent III. Period, Domain / Range & Asymptotes of tan & cot. A) Period = B) Domain (the x values). All values except 1) tan: x /2, 3 /2, 5 /2, etc. (or - /2, -3 /2, etc.) 2) cot: x 0, , 2 , 3 , etc. (or , -2 , etc.) C) Range: (the y values) both are all real numbers. 1) (- ,+ ) or Range = {R} D) Vertical asymptotes (lines graphs never cross). 1) tan: x = /2+ n (x = /2, x = 3 /2, x = 5 /2, etc) 2) cot: x = n (x = 0, x = , x = 2 , etc.)
Graphs of Tangent & Cotangent IV. Transformations of Tangent & Cotangent functions. Standard form: y = D + A trig B(x + C) A) Vertical asymptote shift: 1) set Bx = the normal vertical asymptotes . Solve for x, this is the period shifted asymptotes. a) tan: Bx = - /2 and Bx = /2 b) cot: Bx = 0 and Bx = B) Horizontal & Vertical shifts (same as other trig). 1) Change the sign of the C. This is the sideways shift. 2) The D is the vertical shift (move the graph up/down).