Hidden Markov Models: Understanding State Transition Probabilities
Hidden Markov Models (HMM) are powerful tools used to model systems where states are not directly observable but can be inferred from behaviors. With a focus on state transition probabilities, HMM allows for the estimation of current states based on previous observations. This concept is illustrated through various Markov Model examples and the Bayesian Knowledge Tracing model, highlighting the essence of probabilistic inference in predicting states. Through HMM, the dynamics of systems can be analyzed even when states are hidden, enabling a wide range of applications in fields such as machine learning, speech recognition, and bioinformatics.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Week 8 Video 3 Hidden Markov Models
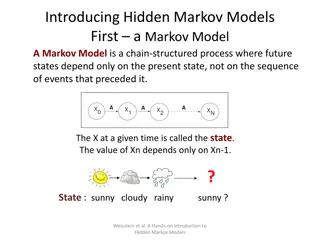
Markov Model There are N states The agent or world (example: the learner) is in only one state at a time At each change in time, the system can change state Based on the current state, there is a different probability for each next state
Markov Model Example 0.3 0.3 0.5 A B 0.3 0.4 0.7 0.2 0.1 C 0.2
Markov Model Example 0.3 1.0 0.5 A B 0.0 0.0 0.7 0.2 0.1 C 0.2
Markov Assumption For predicting the next state, only the current state matters Often a wrong assumption But a nice way to simplify the math and reduce overfitting!
Hidden Markov Model (HMM) There are Nstates The world (or learner) is in only one state at a time We don t know the state for sure, we can only infer it from behavior(s) and our estimation of the previous state At each change in time, the system can change state Based on the current state, there is a different probability for each next state
Hidden Markov Model Example Behavior 0.1 0.5 0.3 0.3 0.5 A B 0.3 0.7 0.4 0.7 0.2 0.1 C 0.2
We can estimate the state Based on the behaviors we see Based on our estimation of the previous state What is the probability that the state is X, given the probability of the behavior seen the probability of each possible prior state the probability of the transition to X from each possible prior state
A Simple Hidden Markov Model: Bayesian Knowledge Tracing p(T) Not learned Learned p(L0) p(G) 1-p(S) correct correct
Hidden Markov Model: BKT There are 2states The world (or learner) is in only one state at a time: KNOWN OR UNKNOWN We don t know the state for sure, we can only infer it from CORRECTNESS and our estimation of the previous probability of KNOWN versus UNKNOWN At each change in time, the system can LEARN Based on the current state, there is a different probability for each next state P(T) of going KNOWN from UNKNOWN KNOWN from KNOWN
Fitting BKT is hard Fitting HMMs is no easier Often local minima Several algorithms are used to fit parameters, including EM, Baum-Welch, and segmental k-Means Our old friends BiC and AIC are typically used to choose number of nodes
Predicting Transitions Between Student Activities (Jeong & Biswas, 2008)
Studying patterns in dialogue acts between students and (human) tutors (Boyer et al., 2009) 5 states 0: Tutor Lecture 4: Tutor Lecture and Probing 3: Tutor Feedback 1: Student Reflection 2: Grounding
Studying patterns in tactics during online learning sessions (Fincham et al., 2019) 8 tactics for sessions, focus on: videos, summative assessments, formative assessments, content access, meta-cognitive actions, and three behavior blends Fit HMM to find common transitions between tactics For example: content access session much more frequent after formative assessment session than after video watching session
A powerful tool For studying the transitions between states and/or behaviors And for estimating what state a learner (or other agent) is in
Next lecture Reinforcement Learning