Ideal Sampling and Z-Transform in Signal Processing
Explore the concept of ideal sampling in signal processing, learn about the Z-transform, periodic sampling, Fourier transform, and the importance of meeting specific frequency conditions for signal recovery. Don't miss out on the HW problems for Z-transform available on the course website by Friday!
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Notice HW problems for Z-transform at available on the course website due this Friday (9/26/2014) http://sist.shanghaitech.edu.cn/faculty/luoxl/class/2014Fall_DSP/DSPclass.ht m
Lecture 3: Sampling XILIANG LUO 2014/9
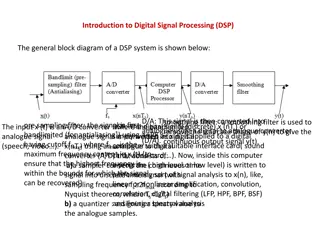
Periodic Sampling A continuous time signal is sampled periodically to obtain a discrete- time signal as: Ideal C/D converter
C/D : Not Invertible in General However, it is possible to reconstruct original signal by restricting the frequency content of the input signal!
Ideal Sampling Impulse train modulator
Fourier Transform of Ideal Sampling Fourier transform of the ideal sampled signal is the convolution of the FT of original continuous signal and the impulse train ??? = ??? {?(?)}
Fourier Transform of Ideal Sampling Fourier Transform of periodic impulse train is an impulse train:
Ideal Sampling Fourier Transform of the ideal sampled signal consists of periodically repeated copies of the Fourier Transform of the original continuous time signal
Observation When Sampling Frequency satisfies the following condition, the replicas of Xc(j ) do not overlap: ? 2 ? When replicas of Xc(j ) do not overlap, ideal lowpass filter will be able to recover original continuous time signal from the ideal sampled signal with the impulse train
Aliasing A simple cosine signal: ??? = cos 0?
Nyquist-Shannon Sampling Let ??(?) be a band-limited signal with Then ??(?) is uniquely determined by its samples if: The frequency ? is referred to as the Nyquiest frequency The frequency 2 ? is called Nyquist rate
What about DTFT This is the general relationship between the periodically sampled sequence and the underlying continuous time signal
Reconstruction If we are given a sequence, we can formulate an impulse train: Let this impulse train be the input to a reconstruction filter
Ideal Band-limited Interpolation
Ideal Reconstruction System Note: output is always bandwidth limited to the cutoff frequency of the lowpass filter
Process Cont. Signal A main application of discrete-time systems is to process continuous- time signal in discrete-time domain
Observations For band-limited signal, we are processing continuous time signal using discrete-time signal processing For band-limited signal, the overall system behaves like a linear time- invariant continuous-time system with the following frequency domain relationship:
Question In order for the following equation to hold, can we allow some aliasing to happen, i.e., the sampling rate is less than the Nyquist rate?
Next 1. Change sampling rate 2. Multi-rate signal processing 3. Quantization 4. Noise shaping
HW Due on 10/10 4.21 4.31 4.34 4.53 4.54 4.60 need multi-rate signal processing knowledge 4.61