Identifying Congruent Triangles and Properties in Geometry
Explore the concept of congruent triangles and properties of parallelograms in geometry. Understand the theorems related to parallelograms and how to determine angles in geometric figures. Discover proofs and constructions to deepen your understanding of these mathematical principles.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
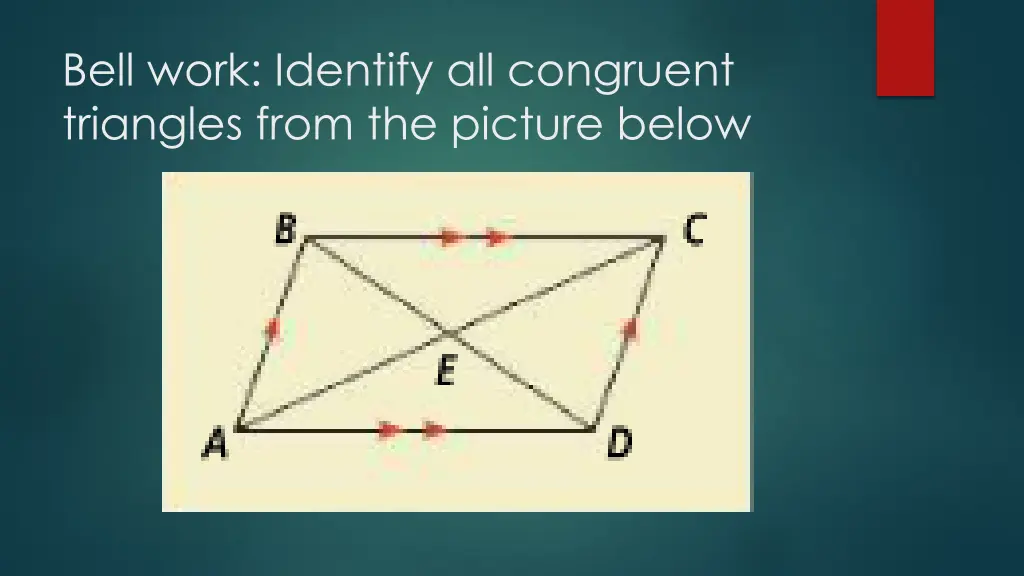
Bell work: Identify all congruent triangles from the picture below
6.2: Properties of Parallelograms
If Statements (AKA Conditional Statements) Recall Theorem 6.2: The sum of the measures of the exterior angles of any polygon is 360
If and Only If statements (AKA Biconditional statements) A triangle has three equal sides if and only if it has three equal angles
Notes A parallelogram is a quadrilateral (4 sided shape) where the opposite sides are all parallel In a quadrilateral, opposite angles are angles that share no side, and opposite sides are sides that share no vertex For any polygon, consecutive angles are angles that are next to each other; ones that share a common side
Theorem 6-3/6-8: A quadrilateral is a parallelogram if and only if its opposite sides are congruent Theorem 6-4/6-9: A quadrilateral is a parallelogram if and only if its consecutive angles are supplementary Theorem 6-5/6-10: A quadrilateral is a parallelogram if and only if its opposite angles are congruent Theorem 6-6/6-11: A quadrilateral is a parallelogram if and only if its diagonals bisect each other
What is the measure of angle P?
If we adjust the lamp such that angle s=86, what would angle R be?
Suppose I construct the diagonals of a parallelogram
In other wordsif we have parallel lines where they are all crossed by the same line, and segments of that line are congruent, then any line that crosses the parallel ones will form segments of the same size
6.3: Proving a quadrilateral is a parallelogram
Find a value for y that makes the shape a parallelogram
For what values of x and y must the shape below be a parallelogram?
Homework: Section 6.2, page 364: 9, 13, 14, 15, 17, 21, 23, 27 Honors: Add 28, 30, 38 Section 6.3, page 372: 7-9, 13 Honors: Add 16, 22, 23
Find the value of each variable or side
Section 6.3 13. Can you prove this is a parallelogram using the given information?
