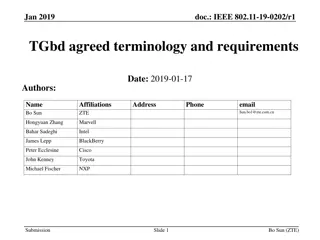
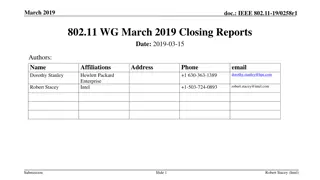
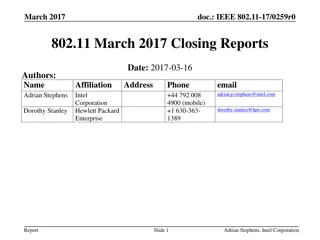
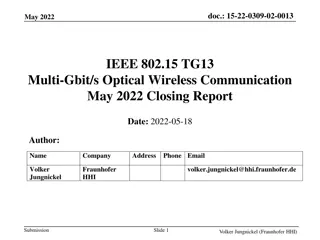
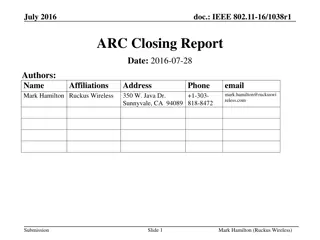
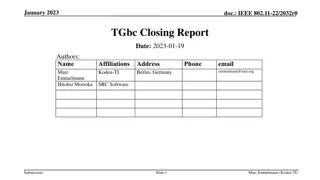
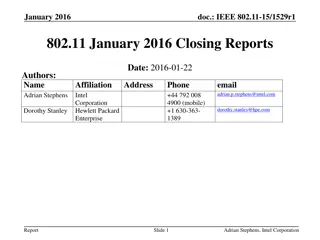
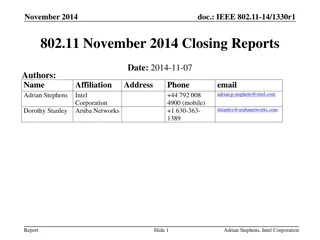
IEEE 802.15 TG6ma January 2023 Closing Report

IEEE 802.15 TG6ma January 2023 Closing Report
Slide Note
Embed
Share

This document contains the closing report for TG15.6ma in January 2023, focusing on the revision of IEEE P802.15.6-2012 with enhanced dependability. The report includes objectives, actions taken, session schedules, and details of the interim session in Baltimore, USA.

  • IEEE
  • TG6ma
  • Closing Report
  • January 2023
  • Wireless Networks
jayly
jayly Follow

Uploaded on Apr 12, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

Download Presentation

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

E N D

Presentation Transcript

  1. Environmental Data Analysis with MATLAB or Python 3rdEdition Lecture 20

  2. SYLLABUS Lecture 01 Lecture 02 Lecture 03 Lecture 04 Lecture 05 Lecture 06 Lecture 07 Lecture 08 Lecture 09 Lecture 10 Lecture 11 Lecture 12 Lecture 13 Lecture 14 Lecture 15 Lecture 16 Lecture 17 Lecture 18 Lecture 19 Lecture 20 Lecture 21 Lecture 22 Lecture 23 Lecture 24 Lecture 25 Lecture 26 Intro; Using MTLAB or Python Looking At Data Probability and Measurement Error Multivariate Distributions Linear Models The Principle of Least Squares Prior Information Solving Generalized Least Squares Problems Fourier Series Complex Fourier Series Lessons Learned from the Fourier Transform Power Spectra Filter Theory Applications of Filters Factor Analysis and Cluster Analysis Empirical Orthogonal functions and Clusters Covariance and Autocorrelation Cross-correlation Smoothing, Correlation and Spectra Coherence; Tapering and Spectral Analysis Interpolation and Gaussian Process Regression Linear Approximations and Non Linear Least Squares Adaptable Approximations with Neural Networks Hypothesis testing Hypothesis Testing continued; F-Tests Confidence Limits of Spectra, Bootstraps

  3. Goals of the lecture Part 1 Finish up the discussion of correlations between time series Part 2 Examine how the finite observation time affects estimates of the power spectral density of time series

  4. Part 1 Coherence frequency-dependent correlations between time series

  5. Scenario A in a hypothetical region windiness and temperature correlate at periods of a year, because of large scale climate patterns but they do not correlate at periods of a few days

  6. wind speed 1 2 3 time, years temperature 1 2 3 time, years

  7. summer hot and windy winters cool and calm wind speed 1 2 3 time, years temperature 1 2 3 time, years

  8. heat wave not especially windy cold snap not especially calm wind speed 1 2 3 time, years temperature 1 2 3 time, years

  9. in this case times series correlated at long periods but not at short periods

  10. Scenario B in a hypothetical region plankton growth rate and precipitation correlate at periods of a few weeks but they do not correlate seasonally

  11. growth rate 1 2 3 time, years precipitation 1 2 3 time, years

  12. growth rate has no seasonal signal plant growth rate summer drier than winter 1 2 3 time, years precipitation 1 2 3 time, years

  13. growth rate high at times of peak precipitation plant growth rate 1 2 3 time, years precipitation 1 2 3 time, years

  14. in this case times series correlated at short periods but not at long periods

  15. Coherence a way to quantify frequency-dependent correlation

  16. strategy band pass filter the two time series, u(t) and v(t) around frequency, 0 compute their zero-lag cross correlation (large when time series are similar in shape) repeat for many 0 s to create a function c( 0)

  17. band pass filter f(t) has this p.s.d. |f( )|2 2 2 - 0 0 0

  18. evaluate at zero lag t=0 and at many 0 s

  19. Short Cut Fact 1 A function evaluates at time t=0 is equal to the integral of its Fourier Transform Fact 2 the Fourier Transform of a convolution is the product of the transforms

  20. integral over frequency

  21. integral over frequency assume ideal band pass filter that is either 0 or 1 negative frequencies positive frequencies

  22. integral over frequency assume ideal band pass filter that is either 0 or 1 negative frequencies positive frequencies c is real so real part is symmetric, adds imag part is antisymmetric, cancels

  23. integral over frequency assume ideal band pass filter that is either 0 or 1 negative frequencies positive frequencies c is real so real part is symmetric, adds imag part is antisymmetric, cancels interpret intergral as an average over frequency band

  24. integral over frequency can be viewed as an average over frequency (indicated with the overbar)

  25. Two final steps 1. Omit taking of real part in formula (simplifying approximation) 2. Normalize by the amplitude of the two time series and square, so that result varies between 0 and 1

  26. the final result is called Coherence

  27. precipitation A) 5 0 0 200 400 600 800 1000 1200 1400 1600 B) new dataset: 20 T-air 10 0 0 200 400 600 800 1000 1200 1400 1600 C) Water Quality 20 T-water 10 0 0 200 400 600 800 1000 1200 1400 1600 D) Reynolds Channel, Coastal Long Island, New York 34 salinity 32 30 28 0 200 400 600 800 time, days 1000 1200 1400 1600 E) turbidity 20 0 0 200 400 600 800 time, days 1000 1200 1400 1600 F) chlorophyll 20 0 0 200 400 600 800 time, days 1000 1200 1400 1600

  28. precipitation precipitation A) 5 0 0 200 400 600 800 1000 1200 1400 1600 air temperature B) new dataset: 20 T-air 10 0 0 200 400 600 800 1000 1200 1400 1600 water temperature C) Water Quality 20 T-water 10 0 0 200 400 600 800 1000 1200 1400 1600 D) Reynolds Channel, Coastal Long Island, New York salinity 34 salinity 32 30 28 0 200 400 600 800 time, days 1000 1200 1400 1600 E) turbidity turbidity 20 0 0 200 400 600 800 time, days 1000 1200 1400 1600 F) chlorophyl chlorophyll 20 0 0 200 400 600 800 time, days 1000 1200 1400 1600

  29. A) periods near 1 year B) periods near 5 days 1 0.05 precip 0 precip 0 -1 -0.05 -2 400 450 500 550 0 200 400 600 800 1000 1200 1400 1600 4 10 2 T-air T-air 0 0 -2 -4 -10 400 450 500 550 0 200 400 600 800 1000 1200 1400 1600 10 1 T-water T-water 0 0 -1 -10 400 450 500 550 0 200 400 600 800 1000 1200 1400 1600 0.6 10 0.4 salinity salinity 0.2 0 -0.20 -0.4 -10 400 450 500 550 0 200 400 600 800 time, days 1000 1200 1400 1600 time, days 2 -101 turbidity turbidity 0 -2 -2 -4 -3 400 450 500 550 0 200 400 600 800 time, days 1000 1200 1400 1600 time, days -2024 2 chlorophyl chlorophyl 0 -4 -2 -6 400 450 500 550 0 200 400 600 800 time, days 1000 1200 1400 1600 time, days Fig, 9.18. Band-pass filtered water quality measurements from Reynolds Channel (New York) for several years starting January 1, 2006. A) Periods near one year; and B) periods near 5 days. MatLab script eda09_16.

  30. A) periods near 1 year B) periods near 5 days 1 0.05 precip 0 precip 0 -1 -0.05 -2 400 450 500 550 0 200 400 600 800 1000 1200 1400 1600 4 10 2 T-air T-air 0 0 -2 -4 -10 400 450 500 550 0 200 400 600 800 1000 1200 1400 1600 10 1 T-water T-water 0 0 -1 -10 400 450 500 550 0 200 400 600 800 1000 1200 1400 1600 0.6 10 0.4 salinity salinity 0.2 0 -0.20 -0.4 -10 400 450 500 550 0 200 400 600 800 time, days 1000 1200 1400 1600 time, days 2 -101 turbidity turbidity 0 -2 -2 -4 -3 400 450 500 550 0 200 400 600 800 time, days 1000 1200 1400 1600 time, days -2024 2 chlorophyl chlorophyl 0 -4 -2 -6 400 450 500 550 0 200 400 600 800 time, days 1000 1200 1400 1600 time, days Fig, 9.18. Band-pass filtered water quality measurements from Reynolds Channel (New York) for several years starting January 1, 2006. A) Periods near one year; and B) periods near 5 days. MatLab script eda09_16.

  31. B) C) A) precipitation and salinity air-temp and water-temp water-temp and chlorophyll 1 1 1 one year coherence coherence coherence 0.5 0.5 0.5 one year one week 0 0 0 0 0.05 0.1 0.15 0.2 0 0.05 0.1 0.15 0.2 0 0.05 0.1 0.15 0.2 frequency, cycles per day frequency, cycles per day frequency, cycles per day

  32. high coherence at periods of 1 year B) C) A) precipitation and salinity air-temp and water-temp water-temp and chlorophyll 1 1 1 one year coherence coherence coherence 0.5 0.5 0.5 one year one week 0 0 0 0 0.05 0.1 0.15 0.2 0 0.05 0.1 0.15 0.2 0 0.05 0.1 0.15 0.2 frequency, cycles per day frequency, cycles per day frequency, cycles per day moderate coherence at periods of about a month very low coherence at periods of months to a few days

  33. Part 2 windowing time series before computing power- spectral density

  34. 1 10 ASD of d d(t) 0 5 scenario: you are studying an indefinitely long phenomenon -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 10 1 ASD of d ASD of W d(t) 0 5 5 W(t) 0 -1 0 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz frequency f, Hz but you only observe a short portion of it 1 1 4 5 ASD of W ASD of Wd) W(t)*d(t) W(t) 0 0 2 -1 0 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz frequency f, Hz 1 4 ASD of Wd) W(t)*d(t) 0 2 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz

  35. how does the power spectral density of the short piece differ from the p.s.d. of the indefinitely long phenomenon (assuming stationary time series)

  36. 1 10 ASD of d d(t) 0 5 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 1 1 10 10 ASD of d ASD of d ASD of W 5 5 5 d(t) d(t) 0 0 W(t) 0 -1 -1 0 0 -1 0 0 200 time t, s time t, s 400 400 0 0 0.1 0.1 0.2 0.2 0.3 0.3 0.4 0.4 0 200 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 We might suspect that the difference will be increasingly significant as frequency f, Hz frequency f, Hz frequency f, Hz 1 1 1 4 5 5 ASD of W the window of observation ASD of Wd) becomes so short that it includes just a few oscillations of the period of interest. 2 ASD of W W(t)*d(t) W(t) 0 W(t) 0 0 2 -1 0 -1 -1 0 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 0 0 200 400 400 0 0 0.1 0.1 0.2 0.2 0.3 0.3 0.4 0.4 200 time t, s time t, s frequency f, Hz frequency f, Hz frequency f, Hz 1 4 4 1 ASD of Wd) ASD of Wd) W(t)*d(t) W(t)*d(t) 0 2 0 -1 -1 0 0 0 200 time t, s time t, s 400 400 0 0 0.1 0.1 0.2 0.2 0.3 0.3 0.4 0.4 0 200 frequency f, Hz frequency f, Hz

  37. starting point short piece is the indefinitely long time series multiplied by a window function, W(t)

  38. 1 10 ASD of d d(t) 0 5 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 ASD of W 5 W(t) 0 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 4 ASD of Wd) W(t)*d(t) 0 2 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz

  39. by the convolution theorem Fourier Transform of short piece is Fourier Transform of indefinitely long time series convolved with Fourier Transform of window function

  40. so Fourier Transform of short piece exactly Fourier Transform of indefinitely long time series when Fourier Transform of window function is a spike

  41. 1 10 ASD of d d(t) 0 5 -1 boxcar window function 0 its Fourier Transform 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 ASD of W 5 W(t) 0 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 4 ASD of Wd) W(t)*d(t) 0 2 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz

  42. 1 10 ASD of d d(t) 0 5 -1 0 boxcar window function its Fourier Transform 0 200 time t, s 400 0 0.1 0.2 sinc() function sort of spiky but has side lobes 0.3 0.4 frequency f, Hz 1 ASD of W 5 W(t) 0 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 4 ASD of Wd) W(t)*d(t) 0 2 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz

  43. 1 10 ASD of d d(t) 0 5 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 ASD of W 5 W(t) 0 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 4 ASD of Wd) W(t)*d(t) 0 2 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz

  44. Effect 1: broadening of spectral peaks 1 narrow spectral peak 10 ASD of d d(t) 0 5 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 wide central spike ASD of W 5 W(t) 0 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 4 wide spectral peak ASD of Wd) W(t)*d(t) 0 2 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz

  45. Effect 2: spurious side lobes 1 only one spectral peak 10 ASD of d d(t) 0 5 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 side lobes ASD of W 5 W(t) 0 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 4 spurious spectral peaks ASD of Wd) W(t)*d(t) 0 2 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz

  46. Q: Can the situation be improved? A: Yes, by choosing a smoother window function more like a Normal Function (which has no side lobes) but still zero outside of interval of observation

  47. 1 10 1 ASD of d 10 ASD of d d(t) 0 5 d(t) 0 5 -1 boxcar window function 0 0 -1 Hamming window function 0 0 200 time t, s 400 0.1 0.2 200 time t, s 0.3 0.4 400 0 0 0.1 0.2 0.3 0.4 frequency f, Hz frequency f, Hz 1 1 4 ASD of W ASD of W 5 W(t) 0 W(t) 0 2 -1 0 -1 0 0 200 time t, s 400 0 0.1 0.2 200 time t, s 0.3 0.4 400 0 0 0.1 0.2 0.3 0.4 frequency f, Hz frequency f, Hz 1 4 1 2 ASD of Wd) ASD of Wd) W(t)*d(t) W(t)*d(t) 0 0 2 1 -1 0 -1 0 0 0.2 200 time t, s 0.4 400 0 0.1 0.2 0.3 0.4 0 200 time t, s 400 0 0.1 0.3 frequency f, Hz frequency f, Hz

  48. 1 10 ASD of d d(t) 0 5 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 4 ASD of W W(t) 0 2 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 2 ASD of Wd) W(t)*d(t) 0 1 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz

  49. 1 10 ASD of d d(t) 0 5 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz 1 4 ASD of W W(t) 0 2 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 no side lobes but central peak wider than with boxcar 0.4 frequency f, Hz 1 2 ASD of Wd) W(t)*d(t) 0 1 -1 0 0 200 time t, s 400 0 0.1 0.2 0.3 0.4 frequency f, Hz

Related


IEEE 802.11 Working Group Session Reports - January 2021

IEEE 802.11 Working Group Session Reports - January 2021

junaid
IEEE 802.11-19-0202/r1 TGbd Agreed Terminology and Requirements

IEEE 802.11-19-0202/r1 TGbd Agreed Terminology and Requirements

valerio
IEEE 802.11-19/0258r1 March 2019 Closing Reports

IEEE 802.11-19/0258r1 March 2019 Closing Reports

indira
Procedures for Closing and Declaring Polls in an Election

Procedures for Closing and Declaring Polls in an Election

saryn
Summary of IEEE 802.11 March 2017 Closing Reports

Summary of IEEE 802.11 March 2017 Closing Reports

adry_30
MAC Performance Evaluation of Multiple BAN Coexistence Under TG6ma Channel Model

MAC Performance Evaluation of Multiple BAN Coexistence Under TG6ma Channel Model

hbout
The Selling Process: Closing Techniques and Strategies

The Selling Process: Closing Techniques and Strategies

cha_kr
Guide to Successful RAD Closing for Public Housing Conversions - Training Insights

Guide to Successful RAD Closing for Public Housing Conversions - Training Insights

echam
IEEE 802.15 TG13 Optical Wireless Communication Closing Report May 2022

IEEE 802.15 TG13 Optical Wireless Communication Closing Report May 2022

del_ran
IEEE 802.11-16/1038r1 ARC Closing Report Summary

IEEE 802.11-16/1038r1 ARC Closing Report Summary

dura_134
IEEE 802.11-22/2032r0 TGbc Closing Report

IEEE 802.11-22/2032r0 TGbc Closing Report

juer376
IEEE 802.11-15 January 2016 Closing Reports

IEEE 802.11-15 January 2016 Closing Reports

mahlay
IEEE 802.11-16/1581r0 January 2017 Closing Reports

IEEE 802.11-16/1581r0 January 2017 Closing Reports

wean555
IEEE 802.11-14/1330r1 November 2014 Closing Reports

IEEE 802.11-14/1330r1 November 2014 Closing Reports

annastac
IEEE 802.11-19/2144r1 Closing Reports January 2020

IEEE 802.11-19/2144r1 Closing Reports January 2020

adylin
Enhanced Dependability in Body Area Networks: May 2024 Report

Enhanced Dependability in Body Area Networks: May 2024 Report

aub_h
IEEE 802.15 Working Group January 2024 Closing Report

IEEE 802.15 Working Group January 2024 Closing Report

lril
IEEE 802.11-23/2133r1 Coex SC Closing Report January 2024

IEEE 802.11-23/2133r1 Coex SC Closing Report January 2024

leib_3
IEEE 802.11 March 2017 Closing Reports

IEEE 802.11 March 2017 Closing Reports

cebreros_d
IEEE 802.15 Working Group Closing Report July 2021 Session

IEEE 802.15 Working Group Closing Report July 2021 Session

ang_f
IEEE 802.11-23-0103r0 1st Vice Chair Report January 2023 Interim

IEEE 802.11-23-0103r0 1st Vice Chair Report January 2023 Interim

jmont
IEEE 802.11-22 January 2023 Session Report

IEEE 802.11-22 January 2023 Session Report

eli_pet

More Related Content