Impact of Cohesive Materials on Gravel Entrainment - Research Study
Explore the influence of cohesive materials like clay, ice, and biological silk on gravel entrainment forces in rivers. The study incorporates laboratory data and field observations to enhance sediment transport predictions and understand channel stability implications. Discover the methodology and results of experiments measuring the impact of clay content and moisture on entrainment forces. Learn about the theoretical model developed to incorporate cohesion forces in predicting grain entrainment.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
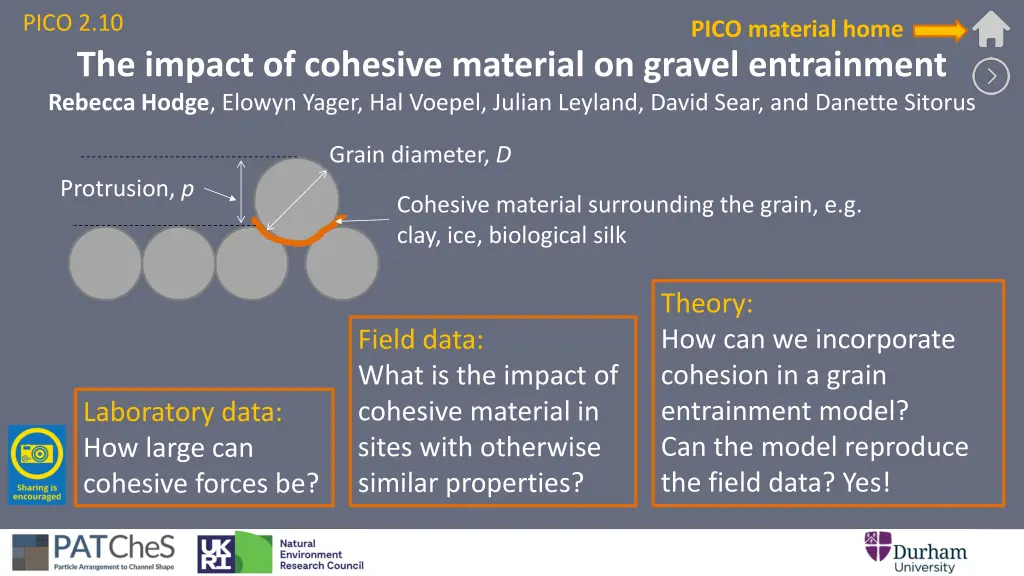
PICO 2.10 PICO material home The impact of cohesive material on gravel entrainment Rebecca Hodge, Elowyn Yager, Hal Voepel, Julian Leyland, David Sear, and Danette Sitorus Grain diameter, D Protrusion, p Cohesive material surrounding the grain, e.g. clay, ice, biological silk Theory: How can we incorporate cohesion in a grain entrainment model? Can the model reproduce the field data? Yes! Field data: What is the impact of cohesive material in sites with otherwise similar properties? Laboratory data: How large can cohesive forces be?
PICO 2.10 The impact of cohesive material on gravel entrainment Rebecca Hodge, Elowyn Yager, Hal Voepel, Julian Leyland, David Sear, and Danette Sitorus PICO material home Motivation Results Motivation Results Methods Summary Methods Summary
Motivation Accurate predictions of critical shear stress ( c) are needed for predicting sediment transport and channel stability in gravel bed rivers. These predictions have implications for instream habitats, flooding, and in- channel engineering. There is increasing understanding of how sediment structure affects c. But, little attention has been paid to the role of commonly occurring cohesive materials in inhibiting grain entrainment. These materials include clay, ice, and biological silk from e.g. caddisflies and mussels. Our aim is to demonstrate the impact that these materials can have on entrainment forces, and to add their effect to an entrainment model.
Methods: Laboratory data Lab experiments were conducted to measure the impact of clay and moisture content on entrainment forces. We mixed trays of water, sand and different proportions of clay (0 to 30%), into which 35 mm marbles were placed. As the trays dried out over several days, the force required to remove the marbles vertically (FL) was measured and the bed moisture content recorded. We calculate a cohesive force per unit grain surface area, CF, as: ??= (?? ??)/?? Where FL is the vertical force to entrain the grain, FW is the weight of the grain, and AC is the buried surface area of the grain. Lift force to entrain grain, FL Cohesive material surrounding the grain, with force per unit area CF Grain weight, FW 4
Methods: Theory To model the horizontal force required to entrain a grain with additional resistance from cohesion, we modify Yager et al. s (2018) force-balance model in which the entrainment force (FR) is ??= ??+ ??+ ??+ ?? where Fg is the force to pivot the weight of the grain out of its pocket, Fs is the force to overcome resistance from overlying sediment, and Fd is the force of intergranular friction and displacement of surrounding sediment. The new term, Fc, is the force produced by cohesive material surrounding the buried grain s surface: ? 2 ??= ?? ??= 2? ? ? ?? where ACis the grain s buried surface area, CF is the cohesion force per surface unit area, D is grain diameter and p is grain protrusion. We assume: 1) that the entire buried surface area is in contact with the cohesive material; 2) the grains are spherical; and 3) cohesive bonds across the entire buried surface have to be broken for the grain to leave its pocket. Grain diameter, D Protrusion, p Cohesive material surrounding the grain, with force per unit area CF 5
Methods: Field data We used a force gauge to measure the horizontal entrainment force required to dislodge grains from an exposed sediment of gravel riverbed. For each grain we also recorded protrusion, diameter, and weight. Data were collected from paired sites to compare entrainment forces from beds that were similar apart from the presence/absence of cohesive material. At one site, Bury Green Brook, we compared measurements from the same areas of the channel, but divided the data by whether clay was observed in the pocket exposed after removing the grain. Maximum horizontal force to dislodge the grain Site without cohesion Site with cohesion Cohesion type Bury Green Brook Bury Green Brook Erlenbach Erlenbach Reynolds Creek Lakefork Chelada North Wash Clay Fines Ice Fines (on bedrock) 6
Methods: Comparing theory and data We evaluate the ability of the theory to reproduce the field data in a two-step process: First, we fit the model to the distribution of forces normalised by grain weight (FR/FW) measured at the site without cohesion by adjusting the distribution of intergranular friction angles ( F). When modelling the force for each individual grain, we sample from this distribution, producing a distribution of possible forces. We then apply the same F distribution to the paired site with cohesion, and adjust the distribution of cohesive forces ( C) until the modelled FR/FW distribution fits the field data. No cohesion site Cohesion site Field data: Grain diameter Protrusion Weight Field data: Grain diameter Protrusion Weight Field Model Field Model Cumulative Cumulative Cumulative Cumulative Cumulative distribution distribution distribution distribution distribution From no cohesion site Adjust to fit Adjust to fit F F C FR/FW FR/FW 7
Results: Laboratory data Clay increases entrainment forces (FL/FW) in drier beds, but its impact is reduced for beds with moisture contents above ~20%. Values of CF (cohesive force per unit surface area) range up to ~30,000 Pa.
Results: Theory FC, calculated using CF value (Pa) Increasing cohesion FR/FR0 Increasing cohesion Weight of overlying sediment Intergranular friction Total force for a grain with no cohesion Grain weight Fc Different components of the entrainment model. For values of CF similar to the laboratory experiments, the cohesion force can be large compared to the other forces. Entrainment force (FR) relative to entrainment force with no cohesion (FR0) for a 50 mm grain. Cohesion has most impact at lower protrusion (p/D < ~0.7).
Results: Field data Distributions of normalised entrainment forces (horizontal force, FC, divided by grain weight, FW) for paired sites. Cohesion increases median FC/FW values by 1.6 to 4.7 times. Reynolds Creek & Lakefork Erlenbach Site without cohesion Bury Green Brook Erlenbach Reynolds Creek Chelada Median FC/FW Median FC/FW Site with cohesion D50, mm D50, mm 40 7.3 33 34.1 Bury Green Brook Erlenbach Lakefork 20 29 4.5 4.7 20 20 17.0 7.8 Chelada & North Wash Bury Green Brook 38 4.7 35 7.8 North Wash
Results: Model fits to data Model reproduces field data well by adjusting distributions of intergranular friction ( F, no cohesion sites) and cohesive force ( C, cohesive sites). Distributions of F are more similar between sites than of C Best fit distributions: Reynolds Creek & Lakefork Erlenbach Chelada & North Wash Bury Green Brook
Results: Critical shear stress Cohesion increases median dimensionless critical shear stress ( *c) by between 1.3 and 6.7 times. Reynolds Creek & Lakefork Erlenbach Chelada & North Wash Bury Green Brook
Summary Cohesive forces from fine sediment and ice can significantly alter entrainment forces and critical shear stress Incorporating cohesive forces into an entrainment model enables field data to be reproduced, and the identified values of CF are comparable to those measured in laboratory experiments. Distributions of intergranular friction are more similar between the different sites than the distributions of cohesion. Here we have used variations on gamma distributions to represent both parameters, which work well.
Future work Cohesive material can increase the resisting force for grain entrainment. However, cohesive material could also the force balance in additional ways: 1) altering sediment structure and hence grain protrusion, and 2) altering near-bed hydraulics. Further work is required to quantify these effects, and the varying impacts of different cohesive materials.






















