Important Terms and Properties of Hyperbola in Co-ordinate Geometry
The lecture covers essential terms related to hyperbola, including center, axes, vertices, latus-rectum, and focal property. It explains the focal property and its proof, defining hyperbola as the locus of a point with constant distances from fixed points.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
2 D Co-ordinate Geometry Lecture-19 The hyperbola Dated:-18.05.2020 PPT-15 UG (B.Sc., Part-1) Dr. Md. Ataur Rahman Guest Faculty Department of Mathematics M.L. Arya, College, Kasba PURNEA UNIVERSITY, PURNIA
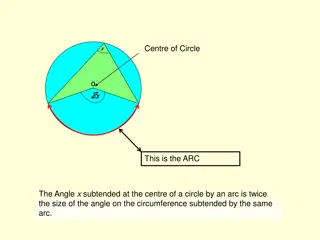
Important terms related to an hyperbola Centre:- The mid-point of the line segment joining the foci of the ellipse is called centre. Here C- centre Axes of the hyperbola: Transverse axis:-The line segment passing through the foci of the hyperbola is called transverse axis. AA transverse axis and AA B K L M' M X A' Z' C A Z S' S(focus) (focus) K' L' B Directrix = 2 a length of transverse axis Conjugate axis:-The line segment passing through the centre and perpendicular to the conjugate axis of the hyperbola. In the figure BB Conjugate axis
Continue Vertices:-The points at which the hyperbola intersects the transverse axis of are called its vertices. In the above figure, A and A are vertices of the hyperbola. Latus-rectum:-The chord passing through the focus and perpendicular to the transverse axis. In the Figure, LL and KK are latus rectum . 2 2 b a = = = and Length of the latus rectum LL KK Note:- In an ellipse Length of transverse-axis Length of conjugate-axis = = 2 AA BB a = = 2 b
The focal property of a hyperbola Property:-The difference of the focal distances of any point on a hyperbola is constant and is equal to the length of the transverse axis of the hyperbola. i.e. If P be a point on the ellipse, then B M' M P(x,y) X A' Z' C A Z S(ae,0) S'(ae,0) B Directrix = = 2 ( a length of transverse axis ) PS PS AA
The focal property of a hyperbola Proof:- Let P(x, y) be any point on the hyperbola 2 2 1....(1) a b x y = 2 2 By the definition, PS PM = e a e = = = ex a ...(2) PS ePM e x a e = = + = ex a + ...(3) PS ePM e x (2) ex a ex a + (3), + = Subtracting PS PS from we get a = = = 2 AA Length of transverse axis
The focal property According to focal property Definition of a hyperbola:-A hyperbola is the locus of a point in a plane such that the difference of its distances from two fixed points in the plane is always constant and is equal to length of transverse-axis. i.e. tan PS PS cons t + = = 2 a
Summary Properties Transverse hyperbola 2 2 1, 0 a b b a e = Conjugate hyperbola x y b a b a e = x y 2 2 = b a = 1, 0 b a 2 2 2 2 ( ) ( ) 2 2 2 1 2 2 2 1 Centre Vertices Foci Length of transverse-axis Length of conjugate-axis (0,0) (0,0) (-a,0) and (a,0) (-ae,0) and (ae,0) (0,-a) and (0,a) (0,-ae) and (0,ae) 2a 2b 2a 2b Eq. of the transverse-axis Eq. of the conjugate-axis Length of the latus-rectum Y=0 X=0 X=0 2 2b a Y=0 2 2b a Eccentricity + 2 2 + 2 2 a b a b = = e e a a